题目内容
以椭圆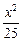 +
+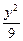 =1的焦点为焦点,离心率e=2的双曲线方程是
=1的焦点为焦点,离心率e=2的双曲线方程是
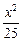 +
+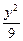 =1的焦点为焦点,离心率e=2的双曲线方程是
=1的焦点为焦点,离心率e=2的双曲线方程是A.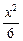 - -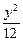 ="1" ="1" | B.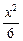 - -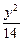 =1 =1 |
C.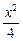 - -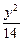 ="1" ="1" | D.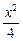 - -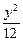 =1 =1 |
D
a2=25,b2=9,则c2=16,c=4,椭圆焦点坐标为(4,0)、(-4,0).
双曲线的焦点仍为(4,0)、(-4,0),由于e=2,c=4,
∴a=2,b2=c2-a2=12.
∴双曲线方程为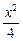 -
-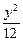 =1.
=1.
双曲线的焦点仍为(4,0)、(-4,0),由于e=2,c=4,
∴a=2,b2=c2-a2=12.
∴双曲线方程为
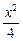 -
-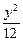 =1.
=1.
练习册系列答案
相关题目
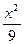 -
-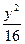 =1只有一个公共点的直线共有______________条.
=1只有一个公共点的直线共有______________条.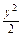 =1于A、B两点,且
=1于A、B两点,且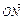 =
=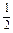 (
(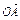 +
+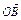 ).
).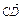 ·
·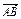 =0,那么A、B、C、D四点是否共圆?为什么?
=0,那么A、B、C、D四点是否共圆?为什么?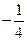
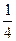
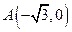 和
和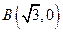 ,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线
,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线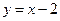 交于D、E两点,求线段DE的长.
交于D、E两点,求线段DE的长.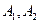 ,垂直于双曲线实轴的直线与双曲线交于
,垂直于双曲线实轴的直线与双曲线交于 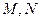 两点,则
两点,则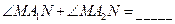
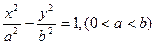 的半焦距为
的半焦距为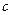 ,直线
,直线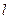 过点
过点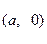 ,
,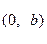 两点.已知原点到直线
两点.已知原点到直线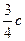 ,则双曲线的离心率为————
,则双曲线的离心率为————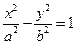
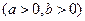 的一个焦点作圆
的一个焦点作圆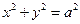 的两条切线,切点分别为A,B,若
的两条切线,切点分别为A,B,若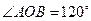 (O是坐标原点),则双曲线线C的离心率为 .
(O是坐标原点),则双曲线线C的离心率为 .