题目内容
9．已知圆O：x2+y2=1，圆C：（x-3）2+（y-4）2=16，则两圆的位置关系为相外切．（从相离、相内切、相外切、相交中选择一个正确答案）分析 根据两圆圆心之间的距离和半径之间的关系进行判断．
解答 解：圆x2+y2=1的圆心O（0，0），半径r=1，
圆（x-3）2+（y-4）2=16，圆心A（3，4），半径R=4，
两圆心之间的距离|AO|=5=4+1=2=R+r，
∴两圆相外切．
故答案：相外切．
点评 本题主要考查圆与圆的位置关系的判断，利用圆心距离和半径之间的关系是解决圆与圆位置关系的主要依据．
练习册系列答案
相关题目
19．为了得到函数$y=\sqrt{2}cos3x$的图象，可以将函数y=$\sqrt{2}$cos$\frac{3}{2}$x的图象所有点的（ ）
| A． | 横坐标伸长到原来的2倍（纵坐标不变）得到 | |
| B． | 横坐标缩短到原来的$\frac{1}{2}$（纵坐标不变）得到 | |
| C． | 纵坐标伸长到原来的2倍（横坐标不变）得到 | |
| D． | 纵坐标缩短到原来的$\frac{1}{2}$（横坐标不变）得到 |
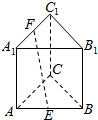正三棱柱ABC-A1B1C1的各棱长都为2，E，F分别为AB、A1C1的中点，则EF的长是$\sqrt{5}$．
