题目内容

1．已知两个等差数列{an}和{bn}的前n项和分别为Sn和Tn，且$\frac{S_n}{T_n}=\frac{2n+30}{n+3}$，则使$\frac{{a}_{n}}{{b}_{n}}$为整数的n值个数为（　　）
A．4B．5C．6D．7

分析 ①当n=1时，$\frac{{a}_{1}}{{b}_{1}}$=$\frac{32}{4}$=8；②当n≥2时，$\frac{{a}_{n}}{{b}_{n}}$=$\frac{{S}_{2n-1}}{{T}_{2n-1}}$=$\frac{2（2n-1）+30}{2n-1+3}$=$\frac{2n+14}{n+1}$=2+$\frac{12}{n+1}$，从而判断即可．

解答 解：①当n=1时，$\frac{{a}_{1}}{{b}_{1}}$=$\frac{32}{4}$=8，故成立；
②当n≥2时，$\frac{{a}_{n}}{{b}_{n}}$=$\frac{{S}_{2n-1}}{{T}_{2n-1}}$=$\frac{2（2n-1）+30}{2n-1+3}$=$\frac{2n+14}{n+1}$=2+$\frac{12}{n+1}$
故n=2，3，5，11；
故使得$\frac{{a}_{n}}{{b}_{n}}$为整数的正整数的个数是4；
故选：B．

点评 本题考查了等差数列前n项和公式的应用及分类讨论的思想应用，属于基础题．

练习册系列答案
相关题目
11．已知函数f（x）=ex-m，g（x）=ln（x+m），其中m＞0
（1）若P（x0，y0）是两个函数图象上的一个公共点，求证：x0=y0；
（2）若P（x0，y0）是两个函数图象上唯一的公共点，求实数m，x0的值；
（3）若两个函数图象无公共点，试问存在几条直线与它们都相切？请说明理由．
12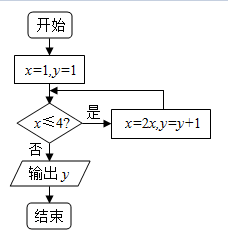．据算法语句（如图）输出的结果是（　　）
A．3B．4C．5D．8
9．已知圆O：x2+y2=1，圆C：（x-3）2+（y-4）2=16，则两圆的位置关系为相外切．（从相离、相内切、相外切、相交中选择一个正确答案）
16．已知M（x0，y0）是双曲线C：$\frac{{x}^{2}}{2}$-y2=1上的一点，F1、F2是C上的两个焦点，若∠F1MF2为钝角，则y0的取值范围是$（-\frac{{\sqrt{3}}}{3}，0）∪（0，\frac{{\sqrt{3}}}{3}）$．
6．若10x=2，则10-3x等于（　　）
A．8B．-8C．$\frac{1}{8}$D．-$\frac{1}{8}$
13．关于x的方程x+log2x=[x]（[x]表示不大于x的最大整数）的解有（　　）个．
A．0B．1C．2D．3
10．已知定义域为R的函数f（x）=$\frac{{-{2^x}+b}}{{{2^{x+1}}+a}}$是奇函数．
（1）求实数a，b的值；
（2）判断函数f（x）的单调性，并说明理由；
（3）若对任意的t∈（1，4），不等式$f（4-k\sqrt{t}）+f（t）＞0$恒成立，求实数k的取值范围．
11．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点到两个焦点的距离分别为3+2$\sqrt{2}$，3-2$\sqrt{2}$，如果直线x=t（t∈R）与椭圆相交于不同的两点A，B，C（-3，0），D（3，0），且直线CA与直线BD的交点是K，试求点K的轨迹方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网