题目内容
10.已知f(x)=ax3+bx2+c的图象经过点(0,1),且在x=1处的切线方程y=x-2.(1)求y=f(x)的解析式;
(2)求y=f(x)的单调递增区间.
分析 (1)先根据f(x)的图象经过点(0,1)求出c,然后根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,建立一等量关系,再根据切点在曲线上建立一等式关系,解方程组即可;
(2)首先对f(x)=5x3-7x2+1求导,可得f'(x)=15x2-14x,令f′(x)>0解之即可求出函数的单调递增区间.
解答 解:(1)f(x)=ax3+bx2+c的图象经过点(0,1),则c=1,
f'(x)=3ax2+2bx,k=f'(1)=3a+2b=1,
切点为(1,-1),
则f(x)=ax3+bx2+c的图象经过点(1,-1),
得a+b+c=-1,
得a=5,b=-7,
则有f(x)=5x3-7x2+1;
(2)f(x)=5x3-7x2+1的导数为
f'(x)=15x2-14x
令f′(x)>0,
解得x<0,或x>$\frac{14}{15}$,
则单调递增区间为(-∞,0),($\frac{14}{15}$,+∞).
点评 本题考查导数的计算与应用,注意导数计算公式的正确运用与导数与单调性的关系,利用导数研究曲线上某点切线方程,属于基础题.

练习册系列答案
相关题目
15.$\frac{co{s}^{2}33°-co{s}^{2}57°}{sin21°-cos21°}$等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
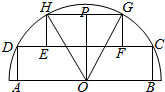 如图,一块半径为2米的半圆形钢板,O为圆心,现从中截出两块内接矩形部件ABCD和EFGH,且HG=2FG,点P为GH的中点,∠POG=θ.
如图,一块半径为2米的半圆形钢板,O为圆心,现从中截出两块内接矩形部件ABCD和EFGH,且HG=2FG,点P为GH的中点,∠POG=θ.