题目内容
6.已知{an}为递增等差数列且a1=1,且a5是a2与a9+10的等比中项.(1)求{an}的通项公式;
(2)设bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$,求{bn}的前n项和Tn;
(3)在(2)条件下对任意n∈N*,Tn>$\frac{m}{23}$都成立,求整数m的最大值.
分析 (1)由题意设{an}的公差为d,且d>0,由等比中项可得(1+4d)2=(1+d)(8d+11),解方程可得d,可得通项公式;
(2)由(1)知bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),裂项相消可得;
(3)由(2)知Tn=$\frac{1}{2+\frac{1}{n}}$,当n=1时Tn取最小值$\frac{1}{3}$,需$\frac{1}{3}$>$\frac{m}{23}$,解不等式可得m的最值.
解答 解:(1)由题意设{an}的公差为d,且d>0,
∵a5是a2与a9+10的等比中项,
∴a52=a2(a9+10),即(1+4d)2=(1+d)(8d+11),
解得d=2,或d=-$\frac{5}{8}$(舍去)
∴{an}的通项公式an=1+2(n-1)=2n-1;
(2)由(1)知bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴{bn}的前n项和Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$;
(3)由(2)知Tn=$\frac{n}{2n+1}$=$\frac{1}{2+\frac{1}{n}}$,随n的增大而增大,
故当n=1时Tn取最小值$\frac{1}{3}$,
要使Tn>$\frac{m}{23}$都成立,需$\frac{1}{3}$>$\frac{m}{23}$,即m<$\frac{23}{3}$,
∴整数m的最大值为7
点评 本题考查数列和不等式的综合应用,涉及裂项法求和以及恒成立问题,属中档题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
| A. | 3(C${\;}_{4}^{1}$C${\;}_{4}^{3}$+C${\;}_{4}^{2}$C${\;}_{4}^{2}$)对 | B. | 3(C${\;}_{8}^{4}$-12)对 | ||
| C. | 3(C${\;}_{8}^{4}$-6)对 | D. | 3C${\;}_{8}^{4}$对 |
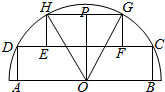 如图,一块半径为2米的半圆形钢板,O为圆心,现从中截出两块内接矩形部件ABCD和EFGH,且HG=2FG,点P为GH的中点,∠POG=θ.
如图,一块半径为2米的半圆形钢板,O为圆心,现从中截出两块内接矩形部件ABCD和EFGH,且HG=2FG,点P为GH的中点,∠POG=θ.