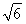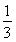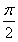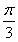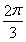题目内容
函数y=f(x),x∈D,若存在常数C,对任意的x1∈D,存在唯一的x2∈D使得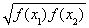 =C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
=C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
A. 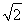 B.2
B.2
C.4 D.2 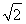
D
【解析】令x1x2=m,且1≤x1≤2,1≤x2≤2,则x2≤x1x2≤2x2,即x2≤m≤2x2,∴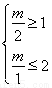 ,可得m=2,故C=
,可得m=2,故C=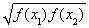 =
=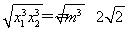

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目