题目内容
(本小题满分12分)
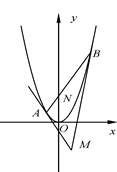
已知过点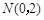 的直线
的直线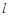 交抛物线
交抛物线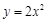 于
于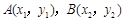 两点,
两点, 为坐标原点.
为坐标原点.
(Ⅰ)求 的面积的最小值;
的面积的最小值;
(Ⅱ)设抛物线在点 处的切线交于点
处的切线交于点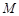 ,求点
,求点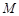 的纵坐标的值.
的纵坐标的值.
已知过点
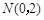 的直线
的直线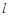 交抛物线
交抛物线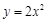 于
于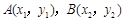 两点,
两点, 为坐标原点.
为坐标原点.
(Ⅰ)求
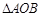 的面积的最小值;
的面积的最小值;(Ⅱ)设抛物线在点
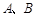 处的切线交于点
处的切线交于点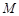 ,求点
,求点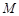 的纵坐标的值.
的纵坐标的值.(Ⅰ)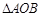 的面积的最小值为2. (Ⅱ)
的面积的最小值为2. (Ⅱ)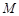 点的纵坐标为
点的纵坐标为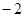 .
.
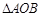 的面积的最小值为2. (Ⅱ)
的面积的最小值为2. (Ⅱ)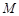 点的纵坐标为
点的纵坐标为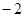 .
. 本试题主要是考查了只想爱你与抛物线的位置关系的综合运用,以及三角形面积的最值的运用。
(1)由题意知直线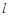 的斜率存在,设
的斜率存在,设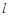 的方程为
的方程为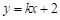 ,然后与抛物线联立方程组得到关于x的方程,结合韦达定理得到面积公式。
,然后与抛物线联立方程组得到关于x的方程,结合韦达定理得到面积公式。
(2)根据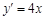 ,
,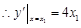 ,得
,得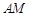 的方程为
的方程为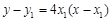 同理得到BM的方程,解得点M的坐标。
同理得到BM的方程,解得点M的坐标。
解:由题意知直线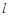 的斜率存在,设
的斜率存在,设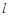 的方程为
的方程为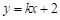 ,
,
联立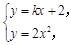 得
得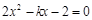 ,∴
,∴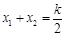 ,
,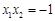 . 2分
. 2分
(Ⅰ)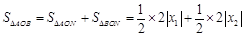 3分
3分
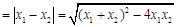 =
=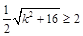 (当
(当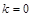 时取“=”) 5分
时取“=”) 5分
所以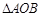 的面积的最小值为2. 6分
的面积的最小值为2. 6分
(其他解法参照给分)
(Ⅱ)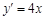 ,
,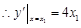 ,得
,得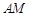 的方程为
的方程为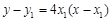 ,
,
即 ,同理
,同理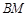 的方程为
的方程为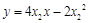 , 8分
, 8分
消去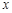 得
得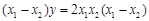 ,
,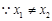 ,
, ,
,
所以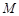 点的纵坐标为
点的纵坐标为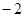 . 12分
. 12分
(1)由题意知直线
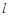 的斜率存在,设
的斜率存在,设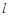 的方程为
的方程为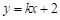 ,然后与抛物线联立方程组得到关于x的方程,结合韦达定理得到面积公式。
,然后与抛物线联立方程组得到关于x的方程,结合韦达定理得到面积公式。(2)根据
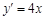 ,
,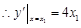 ,得
,得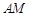 的方程为
的方程为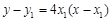 同理得到BM的方程,解得点M的坐标。
同理得到BM的方程,解得点M的坐标。解:由题意知直线
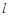 的斜率存在,设
的斜率存在,设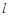 的方程为
的方程为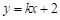 ,
,联立
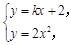 得
得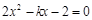 ,∴
,∴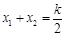 ,
,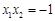 . 2分
. 2分(Ⅰ)
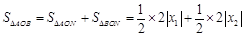 3分
3分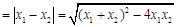 =
=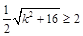 (当
(当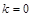 时取“=”) 5分
时取“=”) 5分所以
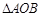 的面积的最小值为2. 6分
的面积的最小值为2. 6分(其他解法参照给分)
(Ⅱ)
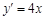 ,
,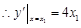 ,得
,得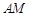 的方程为
的方程为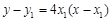 ,
,即
 ,同理
,同理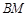 的方程为
的方程为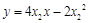 , 8分
, 8分消去
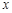 得
得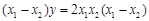 ,
,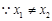 ,
, ,
,所以
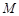 点的纵坐标为
点的纵坐标为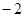 . 12分
. 12分
练习册系列答案
相关题目
 在区间
在区间 上的图像如图所示,则
上的图像如图所示,则 、
、 的值可能是( )
的值可能是( )
 ,
,

 ,
, ,
,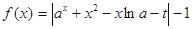
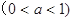 有零点,则实数
有零点,则实数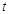 的最小值是( )
的最小值是( ) 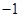
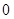

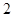
 有( )
有( ) ,极小值
,极小值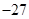

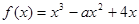 有两个极值点
有两个极值点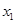 、
、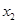 ,且
,且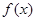 在区间(0,1)上有极大值,无极小值,则
在区间(0,1)上有极大值,无极小值,则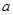 的取值范围是
的取值范围是  的极值点的个数是( ).
的极值点的个数是( ).