题目内容
函数f(x)=x3-ax2-bx+a2,在x=1时有极值10,则a、b的值为( )
| A.a=3,b=-3或a=―4,b=11; | B.a=-4,b=1或a=-4,b="11" ; |
| C.a=-1,b="5" ; | D.以上都不对 |
A
解:因为函数f(x)=x3-ax2-bx+a2,在x=1时有极值10,则利用f’(x)=3x2-2ax-b中x=1导数为零,同时x=1,y=10,联立方程组可知a=3,b=-3或a=―4,b=11 ,经检验都符合题意,选A

练习册系列答案
相关题目
 ;②
;② ;③
;③ .(以上三式中
.(以上三式中 均为常数,且
均为常数,且 )
) ,
, ,求出所选函数
,求出所选函数 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是 ).其中
).其中 表示4月1日,
表示4月1日, 表示5月1日,…,依此类推;
表示5月1日,…,依此类推;
 的单调区间;
的单调区间;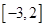 上的最值
上的最值 是
是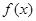 的导函数,
的导函数,
 在
在 处取得极值.
处取得极值. 与
与 满足的关系式;
满足的关系式; ,求函数
,求函数 的单调区间;
的单调区间; ,若存在
,若存在 ,
, ,使得
,使得
 .
. 有两个极值点
有两个极值点 、
、 ,且
,且 在区间(0,1)上有极大值,无极小值,则
在区间(0,1)上有极大值,无极小值,则 的取值范围是( )
的取值范围是( ) 



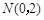 的直线
的直线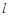 交抛物线
交抛物线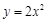 于
于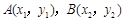 两点,
两点,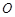 为坐标原点.
为坐标原点.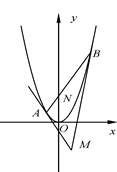
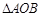 的面积的最小值;
的面积的最小值;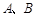 处的切线交于点
处的切线交于点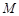 ,求点
,求点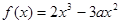 ,
,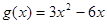 ,又函数
,又函数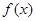 在
在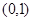 单调递减,而在
单调递减,而在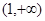 单调递增.
单调递增.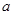 的值;
的值;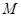 的最小值,使对
的最小值,使对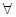
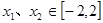 ,有
,有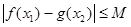 成立;
成立;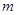 ,使得
,使得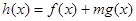 在
在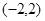 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.