题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为
,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为 ![]()
(1)求椭圆C的方程;
(2)设过点B且斜率为k的动直线l与椭圆C的另一个交点为M, ![]() =λ(
=λ( ![]() ),若点N在圆O上,求正实数λ的取值范围.
),若点N在圆O上,求正实数λ的取值范围.
【答案】
(1)解:由 ![]() ,得
,得 ![]() ,∴a=2b,
,∴a=2b,
∴直线AB的方程为 ![]() ,即x+2y﹣2b=0,
,即x+2y﹣2b=0,
圆心O(0,0)到直线AB的距离为d= ![]() ,∴
,∴ ![]() ,得b=1,
,得b=1,
椭圆C的方程为 ![]()
(2)解:设点M的坐标为(x0,y0)(y0≠0),则点N的坐标为(λx0,λ(y0+1)),
∴ ![]() ,得
,得 ![]() ,
,
又 ![]() ,
,
∴ ![]() ,y0∈(﹣1,1),得
,y0∈(﹣1,1),得 ![]() ,
,
∴正实数λ的取值范围是[ ![]() )
)
【解析】(1)由题意离心率可得a=2b,设出AB所在直线方程,由圆心到直线的距离求得b,则椭圆方程可求;(2)设点M的坐标为(x0 , y0)(y0≠0),由已知向量等式得点N的坐标为(λx0 , λ(y0+1)),结合N在圆上,M在椭圆上,分离参数λ求解.
【考点精析】根据题目的已知条件,利用椭圆的标准方程的相关知识可以得到问题的答案,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

【题目】手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间。
为了解A,B两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A,B两个型号的手机各5台,在相同条件下进行测试,统计结果如下:
手机编号 | 1 | 2 | 3 | 4 | 5 |
A型待机时间(h) | 120 | 125 | 122 | 124 | 124 |
B型待机时间(h) | 118 | 123 | 127 | 120 | a |
已知A,B两个型号被测试手机待机时间的平均值相等。
(Ⅰ)求a的值;
(Ⅱ)求A型号被测试手机待机时间方差和标准差的大小;
(Ⅲ)从被测试的手机中随机抽取A,B型号手机各1台,求至少有1台的待机时间超过122小时的概率。
(注:n个数据![]() …
…![]() 的方差
的方差![]() …
…![]() ,其中
,其中![]() 为数据
为数据![]() …
…![]() 的平均数)
的平均数)
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中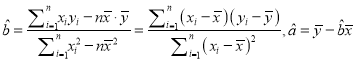 .
.
