题目内容
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(1)求![]() 的解析式;
的解析式;
(2)若对任意的![]() 均有
均有![]() 求实数k的取值范围;
求实数k的取值范围;
(3)设![]() 为两个正数,求证:
为两个正数,求证: ![]()
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)根据导数的几何意义,得到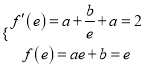 进而求出解析式;(2)研究函数
进而求出解析式;(2)研究函数![]() 的单调性,使得函数的最小值大于0即可;(3)当
的单调性,使得函数的最小值大于0即可;(3)当![]() 时,和
时,和![]() 两种情况;构造函数
两种情况;构造函数![]() 证得
证得![]() ,将式子化简即可。
,将式子化简即可。
解析:
(1)由![]() 得
得![]() ,
,
由题意: 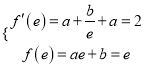 ,解得
,解得![]() ,所以
,所以![]() .
.
(2)令![]() ,
,
则![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]()
![]() 上单调递增,
上单调递增,
所以![]() 的最小值为
的最小值为![]() ,
,
由题意知![]() ,解得
,解得![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() .
.
(3)当![]() 时,结论显然成立,否则不妨设
时,结论显然成立,否则不妨设![]() ,
,
设![]() 则
则![]()
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为减函数;当
上为减函数;当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为增函数.从而当
上为增函数.从而当![]() 时
时![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() 得,
得,
化简得![]() ,
,
故![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目