Question

【题目】已知椭圆的一个顶点为A(0，－1)，焦点在x轴上。若右焦点F到直线x－y＋2＝0的距离为3。

(1)求椭圆的方程；

(2)设直线y＝kx＋m(k≠0)与椭圆相交于不同的两点M、N。当|AM|＝|AN|时，求m的取值范围。

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）根据右焦点到直线x﹣y+=0的距离为3，利用点到直线的距离公式求出c，再由椭圆的一个顶点为A（0，﹣1），求出b，从而得到椭圆方程．（2）设A为弦MN的中点，由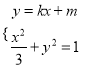，得（3k2+1）x2+6kmx+3（m2﹣1）=0．利用根的判别式和韦达定理，结合题设能求出m的取值范围．

解析：

(1) 设右焦点F（c，0），（c＞0），则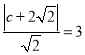，∴．∵椭圆的一个顶点为A（0，﹣1），∴b=1，a2=3，∴椭圆方程是．

（2）设P为弦MN的中点，由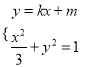得（3k2+1）x2+6kmx+3（m2﹣1）=0．

由△＞0，得m2＜3k2+1 ①，

∴xP=，

从而yP=kxp+m=．

∴kBP=．

由MN⊥AP，得=﹣，

即2m=3k2+1②．

将②代入①，得2m＞m2，

解得0＜m＜2．由②得k2=＞0．

解得m＞．故所求m的取值范围为（，2）．