题目内容

10．已知a、b、c∈R+，且a+b+c=1，求证：$\sqrt{4a+1}$+$\sqrt{4b+1}$+$\sqrt{4c+1}$≤$\sqrt{21}$．

分析 由a、b、c∈R+，且a+b+c=1，运用柯西不等式可得（1•$\sqrt{4a+1}$+1•$\sqrt{4b+1}$+1•$\sqrt{4c+1}$）2≤（12+12+12）（4a+1+4b+1+4c+1），化简整理，即可得证．

解答 证明：由a、b、c∈R+，且a+b+c=1，
运用柯西不等式可得（1•$\sqrt{4a+1}$+1•$\sqrt{4b+1}$+1•$\sqrt{4c+1}$）2
≤（12+12+12）（4a+1+4b+1+4c+1）
=3×（4+3）=21，
当且仅当a=b=c=$\frac{1}{3}$，取得等号．
即有$\sqrt{4a+1}$+$\sqrt{4b+1}$+$\sqrt{4c+1}$≤$\sqrt{21}$．

点评 本题考查不等式的证明，考查柯西不等式的运用，考查运算能力，属于中档题．

练习册系列答案
相关题目
20．已知函数f（x）=Asin（2x+φ）的图象经过点E（$\frac{π}{4}$，$\sqrt{3}$），F（$\frac{π}{3}$，1），其中A≠0，φ∈（0，$\frac{π}{2}$）．
（Ⅰ）求φ的值，并求函数f（x）的单调递增区间；
（Ⅱ）若f（θ）=$\frac{2}{3}$，求sin（$\frac{7π}{6}$-4θ）的值．
1．已知常数a≥0，函数f（x）=ln（1+x）+$\frac{a}{2}$x2-x（x≥0）．
（1）讨论函数f（x）的单调性；
（2）设n∈N*，求证：ln（n+1）＜$\sum_{i=1}^{n}$$\frac{1}{k}$＜ln（n+1）+$\frac{2n-1}{2n}$．
18．如图所示的是一串黑白相间排列的珠子，若按这种规律排列下去，那么第34颗珠子的颜色是（　　）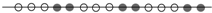
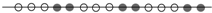
A．白色B．白色的可能性大C．黑色D．黑色的可能性大
5．下面四个命题：
①已知函数$f（x）=\left\{\begin{array}{l}\sqrt{x}\;，x≥0\;\\ \sqrt{-x}\;，x＜0\;\end{array}\right.$且f（a）+f（4）=4，那么a=-4；
②要得到函数$y=sin（{2x+\frac{π}{3}}）$的图象，只要将y=sin2x的图象向左平移$\frac{π}{3}$单位；
③若定义在（-∞，+∞）上的函数f（x）满足f（x+1）=-f（x），则f（x）是周期函数；
④已知奇函数f（x）在（0，+∞）为增函数，且f（-1）=0，则不等式f（x）＜0解集{x|x＜-1}．
其中正确的是③．
15．如图程序框图的算法的意义为9
2．求函数y=$\sqrt{3}$cos2x+sinxcosx的最大值、最小值、周期．
19．如图程序框图中，则输出的A值是$\frac{1}{31}$
20．若sinα=$\frac{3}{5}$，且α是第二象限角，则tanα=（　　）
A．-$\frac{3}{4}$B．$\frac{4}{3}$C．$±\frac{4}{3}$D．$±\frac{3}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网