题目内容
如图,△ABC的角平分线AD的延长线交它的外接圆于点E.
(1)证明:△ABE∽△ADC;
(2)若△ABC的面积S=
AD•AE,求∠BAC的大小.

(1)证明:△ABE∽△ADC;
(2)若△ABC的面积S=
| 1 |
| 2 |

证明:(1)由已知△ABC的角平分线为AD,
可得∠BAE=∠CAD
因为∠AEB与∠ACB是同弧上的圆周角,
所以∠AEB=∠ACD
故△ABE∽△ADC.
(2)因为△ABE∽△ADC,
所以
=
,
即AB•AC=AD•AE.
又S=
AB•ACsin∠BAC,
且S=
AD•AE,
故AB•ACsin∠BAC=AD•AE.
则sin∠BAC=1,
又∠BAC为三角形内角,
所以∠BAC=90°.
可得∠BAE=∠CAD
因为∠AEB与∠ACB是同弧上的圆周角,
所以∠AEB=∠ACD
故△ABE∽△ADC.
(2)因为△ABE∽△ADC,
所以
| AB |
| AE |
| AD |
| AC |
即AB•AC=AD•AE.
又S=
| 1 |
| 2 |
且S=
| 1 |
| 2 |
故AB•ACsin∠BAC=AD•AE.
则sin∠BAC=1,
又∠BAC为三角形内角,
所以∠BAC=90°.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目









 cm
cm cm
cm cm
cm cm
cm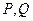 为
为 内的两点,且
内的两点,且 ,
, =
=
 +
+
 ,则
,则 的面积与
的面积与 的面积之比为( )
的面积之比为( )


