题目内容
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组得到的频率分布表如下图所示,

(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
| 班号 | 分组 | 频数 | 频率 |
| 第1组 |  | 5 | 0.050 |
| 第2组 |  | ① | 0.350 |
| 第3组 |  | 30 | ② |
| 第4组 |  | 20 | 0.200 |
| 第5组 |  | 10 | 0.100 |
| 合计 | 100 | 1.00 | |

(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
(1)①应为100×0.35="35," ②应为 ;(2)第3、4、5组中分别抽取3人,2人,1人,进入第二轮面试;(3)
;(2)第3、4、5组中分别抽取3人,2人,1人,进入第二轮面试;(3) .
.
 ;(2)第3、4、5组中分别抽取3人,2人,1人,进入第二轮面试;(3)
;(2)第3、4、5组中分别抽取3人,2人,1人,进入第二轮面试;(3) .
.试题分析:(1)根据频数=样本容量×频率,可分别计算;
(2)分层抽样是按一定的比例进行抽取,因为第3、4、5组人数之比为30:20:10=3:2:1,且共抽取6人,所以第3、4、5组中分别抽取3人,2人,1人,进入第二轮面试;
(3)根据古典概型求概率的公式,先写出基本事件的个数15个,而第4组至少有一名学生被A面试为事件为9个,所以第4组至少有一名学生被考官A面试的概率为
 .
.(1)①应为100×0.35="35," ②应为

(2)∵第3、4、5组人数之比为30:20:10=3:2:1,且共抽取6人,
∴第3、4、5组中分别抽取3人,2人,1人,进入第二轮面试.
(3)设这6人分别为

设第4组至少有一名学生被A面试为事件

所有基本事件为





∴共有15个基本事件
事件
 包含9个基本事件,每个基本时间被抽中是等可能的
包含9个基本事件,每个基本时间被抽中是等可能的∴


练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目


 的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
 ,
,
 ,
,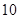
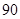 天中抽取
天中抽取 天的数据做进一步分析,每一组应抽取多少天?
天的数据做进一步分析,每一组应抽取多少天?