题目内容
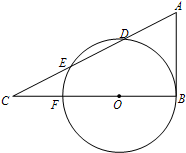
如图，圆O的圆心O在Rt△ABC的直角边BC上，该圆与直角边AB相切，与斜边AC交于D，E，AD=DE=EC，AB=
．
（Ⅰ）求BC的长；
（Ⅱ）求圆O的半径．
| 14 |
（Ⅰ）求BC的长；
（Ⅱ）求圆O的半径．
（Ⅰ）由已知及由切割线定理，
有AB2=AD•AE=
AC•
AC，
所以AC2=
AB2．…（3分）
由勾股定理得，
BC=
=7．…（5分）
（Ⅱ）设圆O与BC的交点为F，圆O的半径为r．
由割线定理，
得CF•CB=CE•CD=
AC•
AC=AB2，…（8分）
即（7-2r）×7=14，
解得r=
．…（10分）
有AB2=AD•AE=
| 1 |
| 3 |
| 2 |
| 3 |
所以AC2=
| 9 |
| 2 |
由勾股定理得，
BC=
| AC2-AB2 |
（Ⅱ）设圆O与BC的交点为F，圆O的半径为r．
由割线定理，
得CF•CB=CE•CD=
| 1 |
| 3 |
| 2 |
| 3 |
即（7-2r）×7=14，
解得r=
| 5 |
| 2 |
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
，即每16人抽取一个人.在1～16中随机抽取一个数，如果抽到的是7，则从33～48这16个数中应取的数是（ ）
