题目内容
【题目】设函数f(x)= ![]() x2+ax﹣lnx(a∈R). (Ⅰ)当a=1时,求函数f(x)的极值;
x2+ax﹣lnx(a∈R). (Ⅰ)当a=1时,求函数f(x)的极值;
(Ⅱ)当a>1时,讨论函数f(x)的单调性;
(Ⅲ)若对任意a∈(3,4)及任意x1 , x2∈[1,2],恒有 ![]() m+ln2>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
m+ln2>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
【答案】解:(Ⅰ)函数的定义域为(0,+∞) 当a=1时,f(x)=x﹣lnx,则f′(x)= ![]()
令f′(x)>0,可得x<0或x>1,∵x>0,∴x>1;
令f′(x)<0,可得0<x<1,∵x>0,∴0<x<1;
∴x=1时,函数f(x)取得极小值为1;
(Ⅱ)f′(x)= 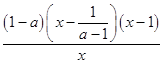
当 ![]() ,即a=2时,
,即a=2时, ![]() ,f(x)在(0,+∞)上是减函数;
,f(x)在(0,+∞)上是减函数;
当 ![]() ,即a>2时,令f′(x)<0,得
,即a>2时,令f′(x)<0,得 ![]() 或x>1;令f′(x)>0,得
或x>1;令f′(x)>0,得 ![]()
当 ![]() ,即1<a<2时,令f′(x)<0,得0<x<1或x>
,即1<a<2时,令f′(x)<0,得0<x<1或x> ![]() ;令f′(x)>0,得
;令f′(x)>0,得 ![]()
综上,当a=2时,f(x)在定义域上是减函数;
当a>2时,f(x)在(0, ![]() )和(1,+∞)上单调递减,在(
)和(1,+∞)上单调递减,在( ![]() ,1)上单调递增;
,1)上单调递增;
当1<a<2时,f(x)在(0,1)和( ![]() ,+∞)上单调递减,在(1,
,+∞)上单调递减,在(1, ![]() )上单调递增;
)上单调递增;
(Ⅲ)由(Ⅱ)知,当a∈(3,4)时,f(x)在[1,2]上单调递减
∴当x=1时,f(x)有最大值,当x=2时,f(x)有最小值
∴ ![]()
∴对任意a∈(3,4),恒有 ![]()
∴m> ![]()
构造函数 ![]() ,则
,则 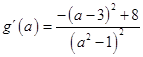
∵a∈(3,4),∴ 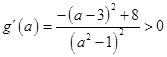
∴函数 ![]() 在(3,4)上单调增
在(3,4)上单调增
∴g(a)∈(0, ![]() )
)
∴m≥ ![]() .
.
【解析】(Ⅰ)确定函数的定义域,利用导数的正负,确定函数的单调性,从而可求函数的极值;(Ⅱ)求导函数f′(x)= ![]() ,分类讨论,利用导数的正负,确定函数的单调性; (Ⅲ)由(Ⅱ)知,当a∈(3,4)时,f(x)在[1,2]上单调递减,从而可得
,分类讨论,利用导数的正负,确定函数的单调性; (Ⅲ)由(Ⅱ)知,当a∈(3,4)时,f(x)在[1,2]上单调递减,从而可得 ![]() 对任意a∈(3,4),恒有
对任意a∈(3,4),恒有 ![]() ,等价于m>
,等价于m> ![]() ,求出右边函数的值域,即可求得结论.
,求出右边函数的值域,即可求得结论.

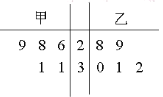
【题目】甲、乙两人在相同条件下各打靶10次,每次打靶所得的环数如图所示.
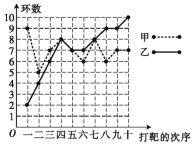
填写下表,请从下列角度对这次结果进行分析.
命中9环及以上的次数 | 平均数 | 中位数 | 方差 | |
甲 | ||||
乙 |
(1)命中9环及以上的次数(分析谁的成绩好些);
(2)平均数和中位数(分析谁的成绩好些);
(3)方差(分析谁的成绩更稳定);
(4)折线图上两人射击命中环数的走势(分析谁更有潜力).