题目内容
【题目】在正四棱柱ABCD﹣A1B1C1D1中,AB= ![]() ,AA1=2,设四棱柱的外接球的球心为O,动点P在正方形ABCD的边上,射线OP交球O的表面于点M,现点P从点A出发,沿着A→B→C→D→A运动一次,则点M经过的路径长为( )
,AA1=2,设四棱柱的外接球的球心为O,动点P在正方形ABCD的边上,射线OP交球O的表面于点M,现点P从点A出发,沿着A→B→C→D→A运动一次,则点M经过的路径长为( )
A.![]()
B.2 ![]() π
π
C.![]()
D.4 ![]() π
π
【答案】A
【解析】解:由题意,点P从点A出发,沿着A→B→C→D→A运动一次,则点M经过的路径是四段大圆上的相等的弧. ∵正四棱柱ABCD﹣A1B1C1D1中,AB= ![]() ,AA1=2,
,AA1=2,
∴四棱柱的外接球的直径为其对角线,长度为 ![]() =2
=2 ![]() ,
,
∴四棱柱的外接球的半径为 ![]() ,∴∠AOB=
,∴∠AOB= ![]() ,
,
∴AB所在大圆,所对的弧长为 ![]() =
= ![]() ,
,
∴点M经过的路径长为 ![]() .
.
故选:A.

练习册系列答案
相关题目
【题目】甲、乙两人在相同条件下各打靶10次,每次打靶所得的环数如图所示.
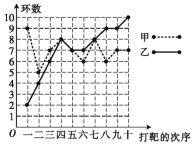
填写下表,请从下列角度对这次结果进行分析.
命中9环及以上的次数 | 平均数 | 中位数 | 方差 | |
甲 | ||||
乙 |
(1)命中9环及以上的次数(分析谁的成绩好些);
(2)平均数和中位数(分析谁的成绩好些);
(3)方差(分析谁的成绩更稳定);
(4)折线图上两人射击命中环数的走势(分析谁更有潜力).
