题目内容
【题目】重庆一中为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的![]() 赛,
赛,![]() 两队各由4名选手组成,每局两队各派一名选手
两队各由4名选手组成,每局两队各派一名选手![]() ,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛
,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛![]() 队选手获胜的概率均为
队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时
,且各局比赛结果相互独立,比赛结束时![]() 队的得分高于
队的得分高于![]() 队的得分的概率为( )
队的得分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:分三种情况求解:即A队5分B队0分;A队4分B队1分;A队3分B队2分,然后根据互斥事件的概率公式可得所求.
详解:(1)A队5分B队0分,即A队四局全胜,概率为![]() .
.
(2)A队4分B队1分,即A队一、二、四局中败1局,第3局胜,
其概率为![]() .
.
(3)A队3分B队2分,包括两种情况:①A队第3局败,其余各局胜;②A队第一、二、四局中胜1局,第3局胜.
其概率为![]() .
.
由互斥事件的概率加法公式可得所求概率为![]() .
.
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两人在相同条件下各打靶10次,每次打靶所得的环数如图所示.
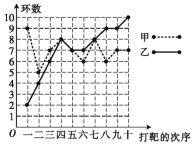
填写下表,请从下列角度对这次结果进行分析.
命中9环及以上的次数 | 平均数 | 中位数 | 方差 | |
甲 | ||||
乙 |
(1)命中9环及以上的次数(分析谁的成绩好些);
(2)平均数和中位数(分析谁的成绩好些);
(3)方差(分析谁的成绩更稳定);
(4)折线图上两人射击命中环数的走势(分析谁更有潜力).
