题目内容
【题目】将数列
中的所有项按第一行排3项，以下每一行比上一行多一项的规则排成如下数表：
……
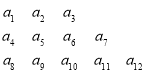
记表中的第一列数
，
，
，…，构成数列
.
（1）设
，求m的值；
（2）若
，对于任何
，都有
，且
.求数列的通项公式.
（3）对于（2）中的数列，若上表中每一行的数按从左到右的顺序均构成公比为q（
）的等比数列，且
，求上表中第k（
）行所有项的和
.
【答案】（1）
（2）
（3）
，
.
【解析】
（1）由题设条件可以知道，
，算出即可；
（2）根据题意知
，因此
，
，…，
将各式相乘得即可得结果；
（3）设上表中每行的公比都为q，表中第1行至第9行共含有数列
的前63项，故
在表中第10行第三列.由此可求出上表中第k（）行所有项的和
.
解（1）由题意，
，
（2）由
，
，
令
得
，且
即
，
所以，因此，，…，，
将各式相乘得；
（3）设上表中每行的公比都为q，且
.因为
，
所以表中第1行至第9行共含有数列的前63项，故在表中第10行第三列，
因此
.又
，所以
，
则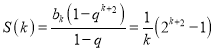
，.
练习册系列答案
相关题目
