题目内容
已知函数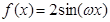 ,其中常数
,其中常数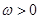 .
.
(1)令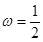 ,求函数
,求函数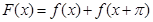 的单调区间;
的单调区间;
(2)令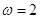 ,将函数
,将函数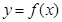 的图像向左平移
的图像向左平移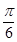 个单位,再往上平移
个单位,再往上平移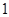 个单位,得到函数
个单位,得到函数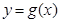 的图像.对任意的
的图像.对任意的 ,求
,求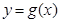 在区间
在区间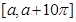 上零点个数的所有可能值.
上零点个数的所有可能值.
(1)增区间 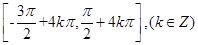 ,减区间
,减区间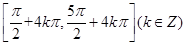 ;
;
(2) 当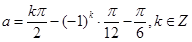 时,21个,否则20个.
时,21个,否则20个.
解析试题分析:(1)令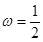 ,函数化为
,函数化为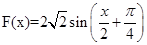 ,可得单调区间;(2)
,可得单调区间;(2)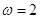 时,经平移可得
时,经平移可得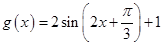 ,根据
,根据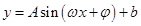 的图像与性质可得零点个数.
的图像与性质可得零点个数.
解:(1) .
.
分别令: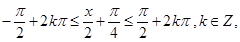 或
或 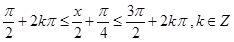 得
得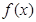 的单调区间;
的单调区间; ,
,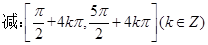 .
.
(2)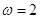 时,
时,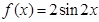 ,
,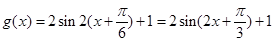 ,
,
其最小正周期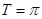 ,
,
由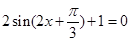 ,得
,得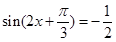 ,
,
∴ ,即
,即 ,
,
区间 的长度为10个周期,
的长度为10个周期,
若零点不在区间的端点,则每个周期有2个零点;
若零点在区间的端点,则仅在区间左或右端点处得一个区间含3个零点,其它区间仍是2个零点;
故当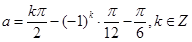 时,21个,否则20个.
时,21个,否则20个.
考点: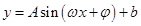 的图像与性质.三角恒等变形.
的图像与性质.三角恒等变形.

练习册系列答案
相关题目
已知函数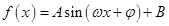 (A>0,ω>0)的一系列对应值如下表:
(A>0,ω>0)的一系列对应值如下表:
| x | 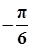 | 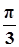 |  | 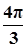 | 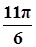 | 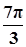 | 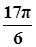 |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果,若函数
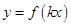 (k>0)周期为
(k>0)周期为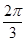 ,当x∈[0,
,当x∈[0,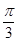 ]时,方程
]时,方程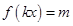 恰有两个不同的解,求实数m的取值范围;
恰有两个不同的解,求实数m的取值范围; 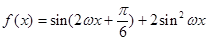 (
(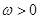 ),其图象的两个相邻对称中心的距离为
),其图象的两个相邻对称中心的距离为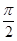 .
.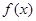 的解析式;
的解析式;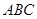 的内角为
的内角为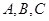 所对的边分别为
所对的边分别为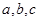 (其中
(其中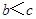 ),且
),且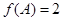 ,
,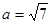 ,
,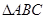 面积为
面积为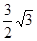 ,求
,求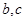 的值.
的值.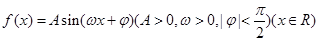 的部分图象如图所示.
的部分图象如图所示.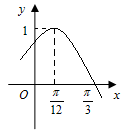
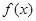 的表达式;
的表达式;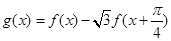 ,求函数
,求函数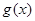 的最小值及相应的
的最小值及相应的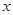 的取值集合.
的取值集合.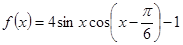 ,求函数
,求函数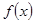 的最小正周期;
的最小正周期; 时,求函数
时,求函数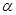 的终边落在直线
的终边落在直线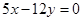 上,求
上,求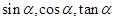 的值。
的值。
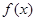 的最小正周期;
的最小正周期;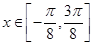 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。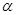 的终边经过点
的终边经过点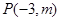 ,且
,且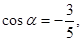
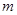 的值.(2)求
的值.(2)求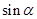 与
与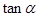 的值.
的值.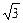 cosωx),其中0<ω<2,函数
cosωx),其中0<ω<2,函数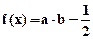 ,其图象的一条对称轴为
,其图象的一条对称轴为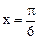 。
。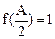 ,b=1,
,b=1,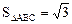 ,求a的值。
,求a的值。