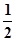题目内容
“点动成线,线动成面,面动成体”。如图, 轴上有一条单位长度的线段
轴上有一条单位长度的线段 ,沿着与其垂直的
,沿着与其垂直的 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的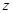 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体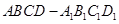 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有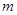 个顶点,
个顶点,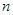 条棱,
条棱, 个面,则
个面,则 的值分别为 ( )
的值分别为 ( )
A. | B.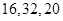 | C.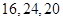 | D.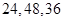 |
A
解析试题分析:依题意,线段AB平移到CD位置后,可形成正方形 ,它有四个顶点、四条棱(边)、一个面;正方形
,它有四个顶点、四条棱(边)、一个面;正方形 平移到正方形
平移到正方形 位置后,可形成正方体
位置后,可形成正方体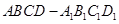 ,它有8个顶点、12条棱、6个面;
,它有8个顶点、12条棱、6个面;
把正方体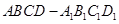 沿着与x轴、y轴、z轴都垂直的第四维方向进行平移得到四维方体后,
沿着与x轴、y轴、z轴都垂直的第四维方向进行平移得到四维方体后,
原来的8个顶点在平移后形成新的8个顶点,所以四维方体就共有8+8=16个顶点;
原先的8个顶点在平移的过程又形成新的8条棱,所以四维方体就共有12+12+8=32条棱;
正方体的12条棱在平移的过程都会形成一个新的面,所以四维方体就共有6+6+12=24个面;正方体的6个面在平移的过程中又各会形成一个正方体,所以四维方体中就包含有1+1+6=8个正方体.
考点:本小题主要考查类比推理.
点评:本题考查利用类比推理来说明空间中点线面之间的形成关系,解题的关键是理解点线面之间的:点动成线,线动成面,面动成体.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
已知几何体M的正视图是一个面积为2 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为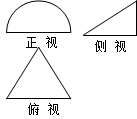
A.6 和 和  | B.6 +4 +4 和 和  |
C.6 +4 +4 和 和  | D.4( + + )和 )和  |
设 是两条直线,
是两条直线, 是两个平面,则
是两个平面,则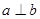 的一个充分条件是( )
的一个充分条件是( )
A.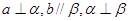 | B.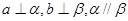 |
C.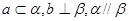 | D.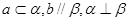 |
 ,则正视图与侧视图中x的值为( )
,则正视图与侧视图中x的值为( )
 .
.
 .
.
 .
.
 .
.
 内的射影构成的图形面积的取值范围是( )
内的射影构成的图形面积的取值范围是( )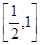

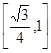
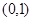
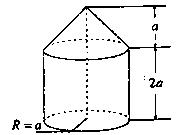


 ,则球的表面积( )
,则球的表面积( ) B、
B、 C、
C、 D、
D、