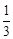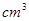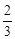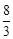题目内容
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的体积是
A. | B. | C. | D.1 |
B
解析试题分析:三视图还原的几何体是四棱锥,一条侧棱垂直底面,画出图形,根据三视图的数据,求出四棱锥的体积。
几何体底面是边长为1的正方形,高是1,其中一条棱与底面垂直的四棱锥,
则它的体积为V=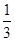 ×1×1×2=
×1×1×2= .故答案为B.
.故答案为B.
考点:考查了三视图的运用
点评:根据三视图能还原几何体,然后结合几何体是四棱锥,分析清楚锥体的高,底面的图形特点,然后结合棱锥的体积公式得到求解,属于基础题。

练习册系列答案
相关题目
已知平面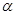 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与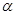 成
成 角的平面
角的平面 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4 、13
、13 ,则球面面积为
,则球面面积为
A.36 | B.48 | C.64 | D.100 |
某几何体的三视图及其相应的度量信息如图所示,则该几何体的表面积为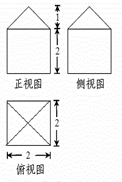
A.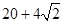 | B. | C.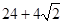 | D.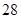 |
正方体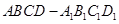 中,
中, 与平面
与平面 所成角的余弦值为( )
所成角的余弦值为( )
A. | B.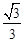 | C. | D.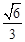 |
一空间几何体的三视图如图,则该几何体的体积为( )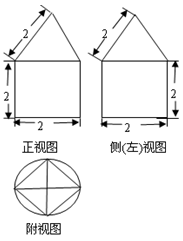
A.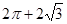 | B.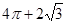 |
C.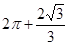 | D.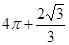 |
一个几何体的三视图如图所示,已知这几何体的体积为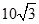 ,则
,则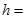 ( )
( )
A.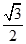 | B.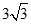 | C. | D. |
 轴上有一条单位长度的线段
轴上有一条单位长度的线段 ,沿着与其垂直的
,沿着与其垂直的 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的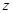 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体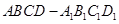 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有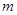 个顶点,
个顶点,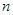 条棱,
条棱, 个面,则
个面,则 的值分别为 ( )
的值分别为 ( )

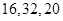
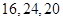
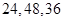
 的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为
的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为




 ),则这个三棱锥的体积是
),则这个三棱锥的体积是