题目内容
球面上有三点A,B,C,其中OA,OB,OC两两互相垂直(O为球心),且过A、B、C三点的截面圆的面积为 ,则球的表面积( )
,则球的表面积( )
A、 B、
B、 C、
C、 D、
D、
A
解析试题分析:因为过A、B、C三点的截面圆的面积为 ,所以在∆ABC中由正弦定理得:
,所以在∆ABC中由正弦定理得: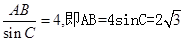 ,又因为OA,OB,OC两两互相垂直,所以
,又因为OA,OB,OC两两互相垂直,所以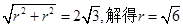 ,所以球的表面积
,所以球的表面积 。
。
考点:球的表面积公式;正弦定理;三棱锥的结构特征。
点评:本题主要考查了学生的抽象概括能力、空间想象能力、运算求解能力以及转化思想,该题灵活性较强,难度较大。该题若直接利用三棱锥来考虑不宜入手,注意到条件中的垂直关系,结合正弦定理来解决。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
如图所示,在正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与直线A1D1,EF,CD都相交的直线( ).
| A.有无数条 | B.有且只有两条 | C.有且只有三条 | D.不存在 |
已知正三角形ABC的边长为a,那么△ABC的平面直观图△A′B′C′的面积为( )
A. a2 a2 | B. a2 a2 | C. a2 a2 | D. a2 a2 |
正方体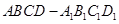 中,
中, 与平面
与平面 所成角的余弦值为( )
所成角的余弦值为( )
A. | B.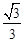 | C. | D.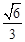 |
 的正方形,主视图与左视图是边长为
的正方形,主视图与左视图是边长为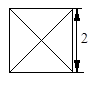




 轴上有一条单位长度的线段
轴上有一条单位长度的线段 ,沿着与其垂直的
,沿着与其垂直的 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的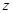 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体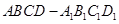 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有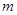 个顶点,
个顶点,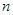 条棱,
条棱, 个面,则
个面,则 的值分别为 ( )
的值分别为 ( )

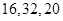
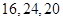
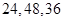


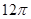







 ,AC=1,则A,B两点在三棱锥的外接球的球面上的距离为( )
,AC=1,则A,B两点在三棱锥的外接球的球面上的距离为( )


