题目内容
正四面体ABCD(六条棱长都相等)的棱长为1,棱AB∥平面,则正四面体上的所有点在平面 内的射影构成的图形面积的取值范围是( )
内的射影构成的图形面积的取值范围是( )
A.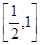 | B. | C.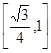 | D.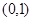 |
B
解析试题分析:因为正四面体的对角线互相垂直,且棱AB∥平面 ,
,
由题意当线段AB相对的侧棱CD与投影面平行时投影面积最大,
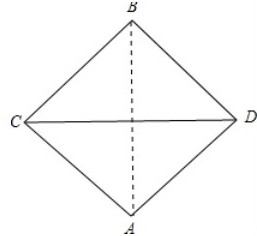
此时投影是一个对角线长等于正四面体棱长1的正方形,如下图所示:
故投影面积为 ,
,
当面CD⊥平面 时,面积取最小值,
时,面积取最小值,
如下图所示:此时构成的三角形底边是1,高是正四面体两条相对棱之间的距离 ,故面积是
,故面积是 ,
,
故图形面积的取值范围是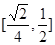 .
.

考点:平行投影及平行投影作图法.
点评:本题考查平行投影及平行投影作图法,本题是一个计算投影面积的题目,注意解题过程中的投影图的变化情况,本题是一个中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
一个几何体的三视图如右图所示,则它的体积为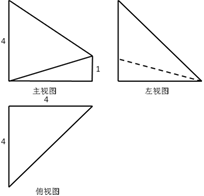
A. | B.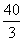 |
C. | D.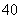 |
若三棱锥的三视图如右图所示,则该三棱锥的体积为【 】.
A. | B.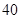 | C.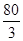 | D. |
一个几何体的三视图如图所示,则该几何体的体积为 ( )
| A.2 | B.1 | C. | D. |
已知正三角形ABC的边长为a,那么△ABC的平面直观图△A′B′C′的面积为( )
A. a2 a2 | B. a2 a2 | C. a2 a2 | D. a2 a2 |
已知平面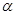 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与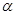 成
成 角的平面
角的平面 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4 、13
、13 ,则球面面积为
,则球面面积为
A.36 | B.48 | C.64 | D.100 |
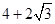 的圆柱形有盖容器中,放入一个半径为3的大球后再放入与球面、圆柱侧面及上底面均相切的小球,则放入的小球的个数最多的为
的圆柱形有盖容器中,放入一个半径为3的大球后再放入与球面、圆柱侧面及上底面均相切的小球,则放入的小球的个数最多的为
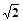
 轴上有一条单位长度的线段
轴上有一条单位长度的线段 ,沿着与其垂直的
,沿着与其垂直的 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的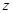 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体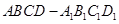 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有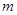 个顶点,
个顶点,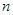 条棱,
条棱, 个面,则
个面,则 的值分别为 ( )
的值分别为 ( )