题目内容
7.设命题p:实数x满足x2-4ax+3a2<0,其中a≠0,命题q:实数x满足$\left\{\begin{array}{l}{{x}^{2}-x-6≤0}\\{{x}^{2}+2x-8>0}\end{array}\right.$.(1)若a=1,且p且q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
分析 (1)当a=1,p且q为真时,则p,q同时为真,建立条件即可求实数x的取值范围;
(2)利用p是q的必要不充分条件,建立条件关系即可求实数a的取值范围.
解答 解:(1)当a=1时,由x2-4x+3<0得1<x<3,即p:1<x<3,
由$\left\{\begin{array}{l}{{x}^{2}-x-6≤0}\\{{x}^{2}+2x-8>0}\end{array}\right.$得$\left\{\begin{array}{l}{-2<x<3}\\{x>2或x<-4}\end{array}\right.$,得2<x<3
q:2<x<3,
∵p且q为真,
∴p,q同时为真,即x满足$\left\{\begin{array}{l}{2<x<3}\\{1<x<3}\end{array}\right.$,
即2<x<3.
由$\left\{\begin{array}{l}{x≤0}\\{{x}^{2}+2x-8>0}\end{array}\right.$,得$\left\{\begin{array}{l}{x≤0}\\{x>2或x<-4}\end{array}\right.$,得x<-4
q:x<-4,
∵p且q为真,
∴p,q同时为真,即x满足$\left\{\begin{array}{l}{x<-4}\\{1<x<3}\end{array}\right.$,
即2<x<3.
(2)∵p是q的必要不充分条件,
∴q是p的充分不必要条件,
由p知,即A={x|a<x<3a,a>0},
由q知,B={x|2<x<3}
∴B?A,
∴$\left\{\begin{array}{l}{a≤2}\\{3a≥3}\end{array}\right.$,
即$\left\{\begin{array}{l}{a≥1}\\{a≤2}\end{array}\right.$,
1≤a≤2
即实数a的取值范围是[1,2].
点评 本题主要考查充分条件和必要条件的应用,利用复合命题之间的关系是解决本题的关键.

| A. | {0,1,2} | B. | {0,1,2,3} | C. | {-2,-1,0} | D. | {-1,0,1,2} |
| A. | 3-$\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 3+$\sqrt{3}$ |
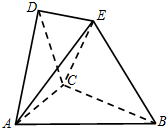 如图,在空间几何体ABCDE中,平面ACD⊥平面ABC,△ABC和△ACD都是边长为2的等边三角形,BE=2,点E在平面ABC内的射影落在∠ABC的平分线上,DE∥平面ABC.
如图,在空间几何体ABCDE中,平面ACD⊥平面ABC,△ABC和△ACD都是边长为2的等边三角形,BE=2,点E在平面ABC内的射影落在∠ABC的平分线上,DE∥平面ABC.