题目内容
18.已知0<x<π,且sin2x=-725,则sin({\frac{π}{4}-x)的值为-45.分析 由条件利用诱导公式,二倍角公式求得sin2(π4−x) 的值,再根据x为钝角,可得sin({\frac{π}{4}-x)<0,从而求得sin({\frac{π}{4}-x)的值.
解答 解:由于sin2x=-725=-cos(2x+π2)=1-2cos2(x+π4)=1-2sin2(π4−x),
∴sin2(π4−x)=1625.
再根据0<x<π,且sin2x=-725=2sinxcosx,可得x为钝角,
∴π4-x∈(-3π4,-π4),∴sin({\frac{π}{4}-x)<0,∴sin({\frac{π}{4}-x)=-45,
故答案为:−45.
点评 本题主要考查诱导公式,二倍角公式的应用,三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
2.若直线ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0所截得的弦长为4,则2a+3b的最小值为( )
| A. | 10 | B. | 4+2√6 | C. | 4+2√3 | D. | 4√6 |
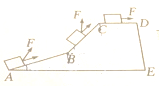 如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=
如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=