题目内容
15.已知函数f(x)=[x[x]],其中[x]表示不超过实数x的最大整数,如[-1.01]=-2,[1.99]=1,若$-\frac{3}{2}≤x<\frac{3}{2}$,则f(x)的值域为( )| A. | {0,1,2} | B. | {0,1,2,3} | C. | {-2,-1,0} | D. | {-1,0,1,2} |
分析 先对x的取值进行分类讨论,从而求出[x]:$-\frac{3}{2}≤x<-1$,-1≤x<0,0≤x<1,$1≤x<\frac{3}{2}$,然后求出对应的x[x]的范围,从而求出x[x]的范围,进而求出f(x)的取值,从而求得f(x)的值域.
解答 解:x=$-\frac{3}{2}$时,[x]=-2,x[x]=3,∴f(x)=3;
$-\frac{3}{2}<x<-1$时,[x]=-2,2<x[x]≤3,∴f(x)=2;
-1≤x<0时,[x]=-1,0<x[x]≤1,∴f(x)=0;
0≤x<1时,[x]=0,x[x]=0,∴f(x)=0;
1≤x<$\frac{3}{2}$时,[x]=1,1$≤x[x]<\frac{3}{2}$,∴f(x)=1;
∴f(x)的值域为{0,1,2,3}.
故选B.
点评 考查对[x]定义的理解,为求x[x]的范围,从而需对x的取值进行分类讨论的方法,以及函数值域的概念.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
5.在北方某城市随机选取一年内100天的空气污染指数(API)的监测数据,统计结果如下:
(Ⅰ)已知污染指数API大于300为重度污染,若本次抽取样本数据有34天是在供暖季,其中有9天为重度污染,完成下面的2×2列联表,问有多大把握认为该城市空气重度污染与供暖有关?
(Ⅱ)某企业由空气污染造成的经济损失S(单位:元)与空气污染指数API(记为ω)的关系式为:S=$\left\{\begin{array}{l}{0,0≤ω≤100}\\{400,100<ω≤300}\\{2000,ω>300}\end{array}\right.$.试估计该企业一个月(30天)内造成的经济损失S的期望
附注:k2=$\frac{n(d-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | (300,+∞) |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 100 |
附注:k2=$\frac{n(d-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.025 | 6.635 | 7.879 | 10.828 |
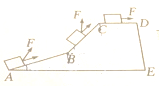 如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.
如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.