Question

【题目】在四面体中，，则四面体体积最大时，它的外接球半径_________．

Answer 1

【答案】

【解析】

由题意画出图形，取AB中点E，连接CE，DE，设AB=2x（0＜x＜1），则CE=DE=，可知当平面ABC⊥平面ABD时，四面体体积最大，写出体积公式，利用导数求得体积最大时的x值，再由△ABD的外心G与△ABC的外心H作两个三角形所在平面的垂线，可得交点O为四面体ABCD的外接球的球心，然后求解三角形得答案．

如图，

取AB中点E，连接CE，DE，

设AB=2x（0＜x＜1），则CE=DE=，

∴当平面ABC⊥平面ABD时，四面体体积最大，

为V===．

V′=，当x∈（0，）时，V为增函数，当x∈（，1）时，V为减函数，

则当x=时，V有最大值．

设△ABD的外心为G，△ABC的外心为H，

分别过G、H作平面ABD、平面ABC的垂线交于O，则O为四面体ABCD的外接球的球心．

在△ABD中，有sin，则cos，

∴sin=．

设△ABD的外接圆的半径为r，则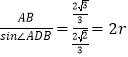，即DG=r=．

又DE=，∴OG=HE=GE=．

∴它的外接球半径R=OD=．

故答案为：．