题目内容
【题目】已知6名某疾病病毒密切接触者中有1名感染病毒,其余5名健康,需要通过化验血液来确定感染者.血液化验结果呈阳性的即为感染者,呈阴性即为健康.
(1)若从这6名密切接触者中随机抽取3名,求抽到感染者的概率;
(2)血液化验确定感染者的方法有:①逐一化验;②分组混合化验:先将血液分成若干组,对组内血液混合化验,若化验结果呈阴性,则该组血液不含病毒;若化验结果呈阳性,则对该组的备份血液逐一化验,直至确定感染者.
(i)采取逐一化验,求所需检验次数![]() 的数学期望;
的数学期望;
(ii)采取平均分组混合化验(每组血液份数相同),依据所需化验总次数的期望,选择合理的平均分组方案.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ;(ii)按(2,2,2)或(3,3)分组进行化验均可.
;(ii)按(2,2,2)或(3,3)分组进行化验均可.
【解析】
(1)总数为![]() ,抽到感染者,则从余下5名某疾病病毒密切接触者中,再抽2人,有
,抽到感染者,则从余下5名某疾病病毒密切接触者中,再抽2人,有![]() ,从而求得抽到感染者的概率;
,从而求得抽到感染者的概率;
(2)分别求出方案(i)和方案(ii)的分布列和均值,注意方案(ii)采取平均分组混合化验,又平均分成3组和平均分成2组两种情况,再通过对比得出结论.
解:(1)从这6名密切接触者中随机抽取3名,共有![]() 种,
种,
抽到感染者,则从余下5名某疾病病毒密切接触者中,再抽2人,有![]()
故抽到感染者的概率![]()
(2)(i)![]() 的可能取值是1,2,3,4,5,且分布列如下:
的可能取值是1,2,3,4,5,且分布列如下:
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
![]()
(ii)首先考虑(3,3)分组,所需化验次数为![]() ,
,![]() 的可能取值是2,3,
的可能取值是2,3,
![]() ,
,
分布列如下:
| 2 | 3 |
|
|
|
![]()
再考虑(2,2,2)分组,所需化验次数为![]() ,
,![]() 的可能取值是2,3,
的可能取值是2,3,
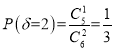 ,
,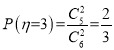
分布列如下:
| 2 | 3 |
|
|
|
![]()
所以按(2,2,2)或(3,3)分组进行化验均可.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.

其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图

以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
【题目】惠州市某学校高三年级模拟考试的数学试题是全国I卷的题型结构,其中第22、23题为选做题,考生只需从中任选一题作答.已知文科数学和理科数学的选做题题目无任何差异,该校参加模拟考试学生共1050人,其中文科学生150人,理科学生900人.在测试结束后,数学老师对该学校全体高三学生选做的22题和23题得分情况进行了统计,22题统计结果如下表1,23题统计结果如下表2.
表1
22题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 70 | 80 | 100 | 500 |
文科人数 | 5 | 20 | 10 | 5 | 70 |
表2
23题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 10 | 10 | 15 | 25 | 40 |
文科人数 | 5 | 5 | 25 | 0 | 5 |
(1)在答卷中完成如下![]() 列联表,并判断能否至少有
列联表,并判断能否至少有![]() 的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
选做22题 | 选做23题 | 合计 | |
文科人数 | 110 | ||
理科人数 | 100 | ||
总计 | 1050 |
(2)在第23题得分为0的学生中,按分层抽样的方法随机抽取6人进行答疑辅导,并在辅导后从这6人中随机抽取2人进行测试,求被抽中进行测试的2名学生均为理科生的概率.
参考公式: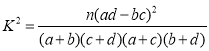 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.