题目内容
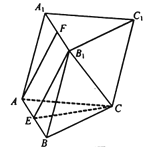
【题目】已知二面角P﹣AB﹣C的大小为120°，且∠PAB＝∠ABC＝90°，AB＝AP，AB+BC＝6．若点P，A，B，C都在同一个球面上，则该球的表面积的最小值为（ ）
A.45πB.
C.
D.
【答案】B
【解析】
设AB＝x，（0＜x＜6），则
，由题意知三棱锥外接球的球心是过△PAB和△ABC的外心E，H，且分别垂直这两个三角形所在平面的垂线的交点O，OB为三棱锥外接球半径，取AB的中点为G，推导出△EGH的外接圆直径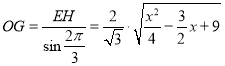
，从而
，当x
时，OB2的最小值为
，由此能求出该球的表面积的最小值．
设AB＝x，（0＜x＜6），则，
由题意知三棱锥外接球的球心是过△PAB和△ABC的外心E，H，
且分别垂直这两个三角形所在平面的垂线的交点O，
OB为三棱锥外接球半径，取AB的中点为G，如图，
由条件知
在△EGH中，由余弦定理可得
∴△EGH的外接圆直径，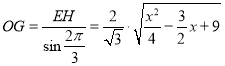
当
时，OB2的最小值为，
∴该球的表面积的最小值为
.
故选：B．
练习册系列答案
相关题目
【题目】某区在2019年教师招聘考试中，参加
、
、
、
四个岗位的应聘人数、录用人数和录用比例（精确到1%）如下：
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
总计 | 533 | 264 | 50% | 467 | 169 | 36% |
（1）从表中所有应聘人员中随机抽取1人，试估计此人被录用的概率；
（2）将应聘岗位的男性教师记为
，女性教师记为
，现从应聘岗位的6人中随机抽取2人.
（i）试用所给字母列举出所有可能的抽取结果；
（ii）设
为事件“抽取的2人性别不同”，求事件发生的概率.
