题目内容
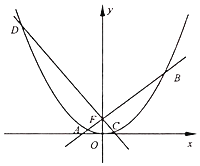
【题目】已知椭圆
的左、右焦点分别为
，
，上顶点为A，过的直线
与y轴交于点M，满足
（O为坐标原点），且直线l与直线
之间的距离为
.
（1）求椭圆C的方程；
（2）在直线
上是否存在点P，满足
？存在，指出有几个这样的点（不必求出点的坐标）；若不存在，请说明理由.
【答案】（1）
；（2）存在两个不同点P，满足
【解析】
（1）根据直线方程求出
和焦点
，计算出椭圆方程的基本量；
（2）求出满足
的点P的轨迹方程，将问题转化为考虑直线与曲线的交点个数问题.
（1）设椭圆C的半焦距为c
因为直线l的方程为
，令
，得
，则点，即
.
令
，得
，则点
由
，得
，解得
，所以
.
所以
所以椭圆C的方程为
（2）存在点P，满足
因为直线
与直线
之间的距离为
，
所以
，解得
或
因为
，所以舍去，故
故直线
的方程为：
设直线上存在点
满足，且点，
，
则
整理得
，它表示圆心在
，半径
的圆
因为圆心到
的距离为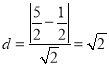
，所以
所以直线与圆
相交，
所以在直线存在两个不同点P，满足
阅读快车系列答案
【题目】空气质量指数AQI是反映空气质量状况的指数，AQI指数值越小，表明空气质量越好，其对应关系如下表：
AQI指数值 | 0～50 | 51～100 | 101～150 | 151～200 | 201～300 | ＞300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势：
下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说，该市10月上旬的空气质量比中旬的空气质量好
【题目】某区在2019年教师招聘考试中，参加
、
、
、
四个岗位的应聘人数、录用人数和录用比例（精确到1%）如下：
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
总计 | 533 | 264 | 50% | 467 | 169 | 36% |
（1）从表中所有应聘人员中随机抽取1人，试估计此人被录用的概率；
（2）将应聘岗位的男性教师记为
，女性教师记为
，现从应聘岗位的6人中随机抽取2人.
（i）试用所给字母列举出所有可能的抽取结果；
（ii）设
为事件“抽取的2人性别不同”，求事件发生的概率.
