题目内容
已知a∈R,设p:函数f(x)=x2+(a-1)x是区间(1,+∞)上的增函数,q:方程x2-ay2=1表示双曲线.
(1)若p为真命题,求实数a的取值范围;
(2)若“p且q”为真命题,求实数a的取值范围.
(1)若p为真命题,求实数a的取值范围;
(2)若“p且q”为真命题,求实数a的取值范围.
(1)[-1,+∞)(2)(0,+∞)
试题分析:(1)因为p为真命题,即函数f(x)=x2+(a-1)x是(1,+∞)上的增函数,由于二次函数单调性决定于对称轴与定义区间的相对位置关系,所以结合图像可得对称轴在区间(1,+∞)左侧时,函数单调增即:
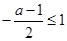 ,解得a≥-1,(2)因为“p且q”为真命题,所以p为真命题,且q也为真命题.由(1)可得p为真命题时有a≥-1;由q为真命题,即方程x2-ay2=1表示双曲线,因而有a>0;两者要同时成立,就是求其交集,为a>0.
,解得a≥-1,(2)因为“p且q”为真命题,所以p为真命题,且q也为真命题.由(1)可得p为真命题时有a≥-1;由q为真命题,即方程x2-ay2=1表示双曲线,因而有a>0;两者要同时成立,就是求其交集,为a>0.试题解析:
(1)因为p为真命题,即函数f(x)=x2+(a-1)x是(1,+∞)上的增函数,
所以
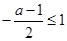 . 3分
. 3分解得a≥-1.
即实数a的取值范围是[-1,+∞). 5分
(2)因为“p且q”为真命题,所以p为真命题,且q也为真命题. 7分
由q为真命题,得a>0.
所以a≥-1且a>0,即a>0.
所以实数a的取值范围是(0,+∞). 10分

练习册系列答案
相关题目
 :函数
:函数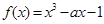 在区间
在区间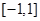 上单调递减;命题
上单调递减;命题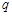 :函数
:函数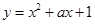 的最小值不大于0.如果命题
的最小值不大于0.如果命题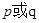 为真命题,
为真命题,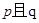 为假命题,求实数
为假命题,求实数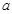 的取值范围.
的取值范围.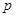 : 关于
: 关于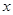 的不等式
的不等式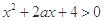 ,对一切
,对一切 恒成立; 命题
恒成立; 命题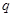 : 函数
: 函数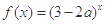 在
在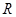 上是增函数.若
上是增函数.若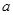 的取值范围.
的取值范围.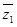 =
=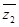
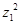 =
=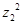
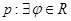 ,使
,使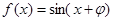 为偶函数;命题
为偶函数;命题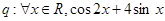
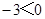 ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )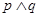


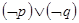
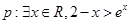 ,命题
,命题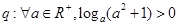 ,则( )
,则( )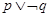 是假命题
是假命题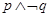 是真命题
是真命题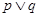 是假命题
是假命题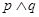 是真命题
是真命题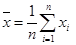 ,
,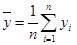 ,则回归直线y=bx+a必过点(
,则回归直线y=bx+a必过点(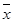 ,
, 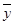 ).
).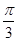 个单位,得到函数y=sin
个单位,得到函数y=sin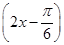 的图象;
的图象;