题目内容
设命题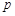 :函数
:函数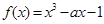 在区间
在区间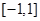 上单调递减;命题
上单调递减;命题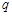 :函数
:函数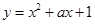 的最小值不大于0.如果命题
的最小值不大于0.如果命题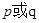 为真命题,
为真命题,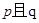 为假命题,求实数
为假命题,求实数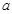 的取值范围.
的取值范围.
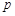 :函数
:函数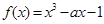 在区间
在区间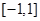 上单调递减;命题
上单调递减;命题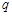 :函数
:函数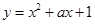 的最小值不大于0.如果命题
的最小值不大于0.如果命题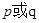 为真命题,
为真命题,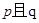 为假命题,求实数
为假命题,求实数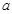 的取值范围.
的取值范围.a∈(-∞,-2]∪[2,3).
试题分析:由p为真命题,能够推导出a≥3.再由q为真命题,能够推导出a≤-2或a≥2.由题意P和q有且只有一个是真命题,所以p真q假?
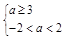 ?a∈ϕ,p假q真?
?a∈ϕ,p假q真?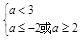
?a≤-2或2≤a<3.由此能够得到a的取值范围.
试题解析:p为真命题?f′(x)=3x2-a≤0在[-1,1]上恒成立?a≥3x2在[-1,1]上恒成立?a≥3.
q为真命题?Δ=a2-4≥0恒成立?a≤-2或a≥2.
由题意p和q有且只有一个是真命题.
p真q假?
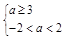 ?a∈∅;
?a∈∅;p假q真?
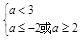 ?a≤-2或2≤a<3.
?a≤-2或2≤a<3.综上所述:a∈(-∞,-2]∪[2,3).

练习册系列答案
相关题目
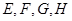 是空间四点,命题甲:
是空间四点,命题甲: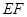 和
和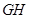 不相交,则甲是乙成立的充分不必要条件;
不相交,则甲是乙成立的充分不必要条件;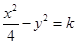 的渐近线方程为
的渐近线方程为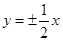 ,则k=1.其中真命题的序号是 .
,则k=1.其中真命题的序号是 .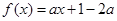 在区间
在区间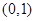 内有零点的充分不必要条件是
内有零点的充分不必要条件是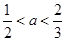 ;②已知
;②已知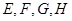 是空间四点,命题甲:
是空间四点,命题甲: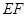 和
和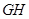 不相交,则甲是乙成立的充分不必要条件;③“
不相交,则甲是乙成立的充分不必要条件;③“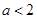 ”是“对任意的实数
”是“对任意的实数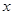 ,
,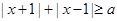 恒成立”的充要条件;④“
恒成立”的充要条件;④“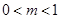 ”是“方程
”是“方程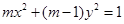 表示双曲线”的充分必要条件.其中所有真命题的序号是 .
表示双曲线”的充分必要条件.其中所有真命题的序号是 .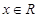 ,都有
,都有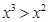 ”的否定是( )
”的否定是( )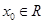 ,使得
,使得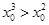
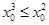
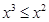
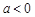 ,则一元二次方程
,则一元二次方程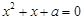 有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )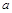 、b、c,若
、b、c,若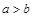 ,则
,则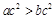
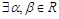 ,使得
,使得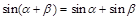 成立
成立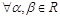 ,
,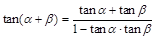 成立
成立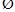 p是____________________.
p是____________________.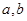 都是奇数,则
都是奇数,则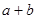 是偶数”的逆否命题是( )
是偶数”的逆否命题是( )