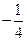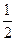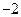题目内容
已知函数f(x)=x3-x
(1)求曲线y=f(x)在点M(t,f(t))处的切线方程
(2)设a>0,如果过点(a,b)可作曲线y=f(x)的三条切线,证明:-a<b<f(a)
(1)求曲线y=f(x)在点M(t,f(t))处的切线方程
(2)设a>0,如果过点(a,b)可作曲线y=f(x)的三条切线,证明:-a<b<f(a)
(1)求函数f(x)的导函数;f'(x)=3x2-1.
曲线y=f(x)在点M(t,f(t))处的切线方程为:y-f(t)=f'(t)(x-t),即y=(3t2-1)x-2t3;
(2)如果有一条切线过点(a,b),则存在t,使b=(3t2-1)a-2t3.
于是,若过点(a,b)可作曲线y=f(x)的三条切线,则方程2t3-3at2+a+b=0有三个相异的实数根.
记g(t)=2t3-3at2+a+b,则g'(t)=6t2-6at=6t(t-a).
当t变化时,g(t),g'(t)变化情况如下表:

由g(t)的单调性,当极大值a+b<0或极小值b-f(a)>0时,方程g(t)=0最多有一个实数根;
当a+b=0时,解方程g(t)=0得t=0,t=
,即方程g(t)=0只有两个相异的实数根;
当b-f(a)=0时,解方程g(t)=0得t=-
,t=a,即方程g(t)=0只有两个相异的实数根.
综上,如果过(a,b)可作曲线y=f(x)三条切线,即g(t)=0有三个相异的实数根,则
即-a<b<f(a).
曲线y=f(x)在点M(t,f(t))处的切线方程为:y-f(t)=f'(t)(x-t),即y=(3t2-1)x-2t3;
(2)如果有一条切线过点(a,b),则存在t,使b=(3t2-1)a-2t3.
于是,若过点(a,b)可作曲线y=f(x)的三条切线,则方程2t3-3at2+a+b=0有三个相异的实数根.
记g(t)=2t3-3at2+a+b,则g'(t)=6t2-6at=6t(t-a).
当t变化时,g(t),g'(t)变化情况如下表:

由g(t)的单调性,当极大值a+b<0或极小值b-f(a)>0时,方程g(t)=0最多有一个实数根;
当a+b=0时,解方程g(t)=0得t=0,t=
| 3a |
| 2 |
当b-f(a)=0时,解方程g(t)=0得t=-
| a |
| 2 |
综上,如果过(a,b)可作曲线y=f(x)三条切线,即g(t)=0有三个相异的实数根,则
|
即-a<b<f(a).

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
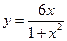 的极大值为 。
的极大值为 。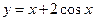 在区间
在区间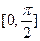 上的最大值是
上的最大值是 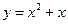 ,则在闭区间
,则在闭区间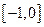 上的最小值是( )
上的最小值是( )