题目内容
已知函数f(x)=
x3-x2+ax+b的图象在点x=0处的切线方程为y=3x-2．
（Ⅰ）求实数a，b的值；
（Ⅱ）设f′（x）≥6，求此不等式的解集．
| 1 |
| 3 |
（Ⅰ）求实数a，b的值；
（Ⅱ）设f′（x）≥6，求此不等式的解集．
（Ⅰ）把x=0代入y=3x-2中，得：y=-2，，则切点坐标为（0，-2），
把（0，-2）代入f（x）中，得：b=-2，
求导得：f′（x）=x2-2x+a，把x=0代入得：f′（0）=a，
又切线方程的斜率k=3，则a=3；
（Ⅱ）把a=3代入导函数得：f′（x）=x2-2x+3，
代入不等式得：x2-2x+3≥6，
变形得：（x-3）（x+1）≥0，
可化为：
或
解得：x≤-1或x≥3，
则原不等式的解集为（-∞，-1]∪[3，+∞）．
把（0，-2）代入f（x）中，得：b=-2，
求导得：f′（x）=x2-2x+a，把x=0代入得：f′（0）=a，
又切线方程的斜率k=3，则a=3；
（Ⅱ）把a=3代入导函数得：f′（x）=x2-2x+3，
代入不等式得：x2-2x+3≥6，
变形得：（x-3）（x+1）≥0，
可化为：
|
|
解得：x≤-1或x≥3，
则原不等式的解集为（-∞，-1]∪[3，+∞）．
练习册系列答案
相关题目
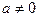，函数
．
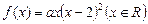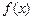有极大值32，求实数
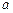的值；(Ⅱ)若对
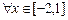，不等式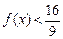
恒成立，求实数
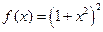的极值情况是： 极大值； 极小值（填“存在”或“不存在”）。