题目内容

12．如图，在正方体ABCD-A1B1C1D1中，O1为底面的中心，则O1A与上底面A1B1C1D1所成角的正切值是（　　）
A．1B．$\frac{{\sqrt{2}}}{2}$C．$\sqrt{2}$D．2$\sqrt{2}$

分析 连结A1C1，则∠AO1A1即为O1A与上底面A1B1C1D1所成角的平面角，利用勾股定理得A1O1，在Rt△AA1O1中利用tan∠AO1A1=$\frac{A{A}_{1}}{{A}_{1}{O}_{1}}$计算即可．

解答 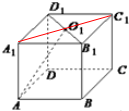解：连结A1C1，则∠AO1A1即为O1A与上底面A1B1C1D1所成角的平面角，
设该正方体的边长为a，则A1C1=$\sqrt{2}$a，
∴A1O1=$\frac{1}{2}$A1C1=$\frac{\sqrt{2}}{2}$a，
在Rt△AA1O1中，tan∠AO1A1=$\frac{A{A}_{1}}{{A}_{1}{O}_{1}}$=$\sqrt{2}$，
故选：C．

点评 本题考查线面角的三角函数值，注意解题方法的积累，属于基础题．

练习册系列答案
相关题目
12．设命题p：x2-3x+2＜0，q：$\frac{x-1}{x-2}$≤0，则p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
13．变量 x，y 满足约束条件$\left\{\begin{array}{l}{x+2y≥2}\\{2x+y≤4}\\{4x-y≥-1}\end{array}\right.$，则z=2x-y的最大值为（　　）
A．-1B．1C．4D．6
10．已知（$\sqrt{x}$+$\frac{x}{2}$）n的展开式中，前三项系数成等差数列，求展开式中含有$\sqrt{{x}^{11}}$的项的二项式系数及项的系数．
7．已知点P（1，3），Q（1，2）．设过点P的动直线与抛物线y=x2交于A，B两点，直线AQ，BQ与该抛物线的另一交点分别为C，D．记直线AB，CD的斜率分
别为k1，k2．
（Ⅰ）当k1=0时，求弦AB的长；
（Ⅱ）当k1≠2时，$\frac{{k}_{2}-2}{{k}_{1}-2}$是否为定值？若是，求出该定值．
17．如图，在四棱椎P-ABCD中，底面ABCD是边长为6的菱形，侧棱PD⊥平面ABCD，BD=6，PD=3$\sqrt{6}$，点E，F分别是PB，CB上靠近点B的一个三等分点．
（Ⅰ）求证：AC⊥DE；
（Ⅱ）求三棱椎F-PAB的高；
（Ⅲ）在线段PC上是否存在一点G，使得FG与平面PDC所成角的正弦值为$\frac{1}{3}$？若存在，请求出CG的长，若不存在，请说明理由．
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且经过点（1，$\frac{\sqrt{2}}{2}$），
（1）求椭圆C的标准方程；
（2）设Q（2，0），过点（-1，0）的直线l交C于M，N两点，△QMN的面积记为S，若对满足条件的任意直线l，不等式S≤λtan∠MQN恒成立，求λ的最小值．
1．（1）已知数列{an}适合：a1=1，an+1=$\frac{2{a}_{n}}{{a}_{n}+2}$，写出前5项并写出其通项公式；
（2）用上面的数列{an}，通过等式bn=an-an+1构造新数列{bn}，写出bn，并写出{bn}的前5项．
2．解关于x的不等式：x2+ax+4＞0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网