Question

5．在地上画一正方形线框，其边长为一枚硬币直径的2倍，向正方形内投硬币，硬币完全落在正方形外的不计，则硬币完全落在正方形内的概率为$\frac{4}{32+π}$．

Answer 1

分析 由题意知本题是一个几何概型，概率等于面积之比，根据题意算出试验包含的总面积和符合条件的面积，两者求比值，得到要求的概率．

解答 解：设硬币的直径为2cm，正方形线框的边长为4．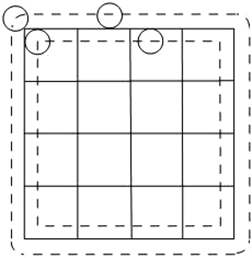
考虑圆心的运动情况．
因为每次投掷都落在最大的正方形内或与最大的正方形有公共点，所以圆心的最大限度为原正方形向外再扩张1个小圆半径的区域，且四角为四分之圆弧；
此时总面积为：
4×4+4×4×1+π×1²=32+π；
完全落在最大的正方形内时，圆心的位置在2为边长的正方形内，
其面积为：2×2=4；
∴硬币落下后完全在最大的正方形内的概率为：P=$\frac{4}{32+π}$，
故答案为：$\frac{4}{32+π}$

点评 本题考查几何概型和求面积的方法，正确理解本题题意是解决本题的关键．难度较大．