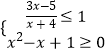题目内容
【题目】己知函数f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),a>0,且a≠1.
(1)若1是关于x的方程f(x)﹣g(x)=0的一个解,求t的值;
(2)当0<a<1且t=﹣1时,解不等式f(x)≤g(x);
(3)若函数F(x)=af(x)+tx2﹣2t+1在区间(﹣1,2]上有零点,求t的取值范围.
【答案】解:(1)∵1是关于x的方程f(x)﹣g(x)=0的一个解,
∴loga2﹣2loga(2+t)=0,
∴2=(2+t)2 ,
∴t=![]() ﹣2;
﹣2;
(2)当0<a<1且t=﹣1时,
不等式f(x)≤g(x)可化为
loga(x+1)≤2loga(2x﹣1),
故![]() ,
,
解得,![]() <x≤
<x≤![]() ;
;
(3)F(x)=af(x)+tx2﹣2t+1
=x+1+tx2﹣2t+1=tx2+x﹣2t+2,
令tx2+x﹣2t+2=0,
即t(x2﹣2)=﹣(x+2),
∵x∈(﹣1,2],∴x+2∈(1,4],
∴t≠0,x2﹣2≠0;
∴![]() =﹣
=﹣![]() =﹣[(x+2)+
=﹣[(x+2)+![]() ]+4,
]+4,
∵2![]() ≤(x+2)+
≤(x+2)+![]() ≤
≤![]() ,
,
∴﹣![]() ≤﹣[(x+2)+
≤﹣[(x+2)+![]() ]+4≤4﹣2
]+4≤4﹣2![]() ,
,
∴﹣![]() ≤
≤![]() ≤4﹣2
≤4﹣2![]() ,
,
∴t≤﹣2或t≥![]() .
.
【解析】(1)由题意得loga2﹣2loga(2+t)=0,从而解得.
(2)由题意得loga(x+1)≤2loga(2x﹣1),由对数函数的单调性可得![]() , 从而解得.
, 从而解得.
(3)化简F(x)=tx2+x﹣2t+2,从而令tx2+x﹣2t+2=0,讨论可得![]() =﹣
=﹣![]() =﹣[(x+2)+
=﹣[(x+2)+![]() ]+4,从而解得.
]+4,从而解得.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.
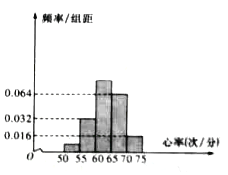
(Ⅰ)求![]() 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;
(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 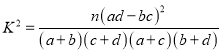 ,其中
,其中![]()
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |