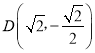题目内容
【题目】已知命题p:存在x0∈R,使![]() ;命题q:对任意x∈R,mx2+mx+1>0;若p∨q为真,p∧q为假,求实数m的取值范围.
;命题q:对任意x∈R,mx2+mx+1>0;若p∨q为真,p∧q为假,求实数m的取值范围.
【答案】(﹣∞,0)∪[2,4)
【解析】
先计算命题![]() 为真时
为真时![]() ;再计算命题
;再计算命题![]() 为真时
为真时![]() ;讨论
;讨论![]() 真
真![]() 假和
假和![]() 假
假![]() 真两种情况计算得到答案.
真两种情况计算得到答案.
若命题p:存在x0∈R,使![]() 为真;
为真;
∴m<(![]() sinx+cosx)max;y
sinx+cosx)max;y![]() sinx+cosx=2sin(x
sinx+cosx=2sin(x![]() ),∴ymax=2;∴m<2.
),∴ymax=2;∴m<2.
故命题p为真m<2;
若命题q:对任意x∈R,mx2+mx+1>0为真;
∴当m=0时,1>0恒成立;当m≠0时,![]() ,解得0<m<4;
,解得0<m<4;
故命题q为真0≤m<4;
∵p∨q为真,p∧q为假;∴p,q中一真一假;
∴![]() 或
或![]() ;∴m<0或2≤m<4.
;∴m<0或2≤m<4.
故实数m的取值范围:(﹣∞,0)∪[2,4).

练习册系列答案
相关题目