题目内容
【题目】如图,已知过点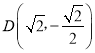 的椭圆
的椭圆![]() 的离心率为
的离心率为![]() ,左顶点和上顶点分别为A,B.
,左顶点和上顶点分别为A,B.
(1)求椭圆的标准方程;
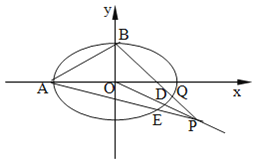
(2)若P为线段OD延长线上一点,直线PA交椭圆于另一点E,直线PB交椭圆于另一点Q.
①求直线PA与PB的斜率之积;
②判断直线AB与EQ是否平行?并说明理由.
【答案】(1)![]() 1.(2) ①
1.(2) ① ![]() .②平行.理由见解析
.②平行.理由见解析
【解析】
(1)离心率值转化为![]() 关系,再把点
关系,再把点![]() 坐标代入方程,即可求出椭圆标准方程;
坐标代入方程,即可求出椭圆标准方程;
(2)①求出![]() 方程,设出
方程,设出![]() 点坐标,可求出直线PA与PB的斜率之积;
点坐标,可求出直线PA与PB的斜率之积;
②求出直线![]() 方程,分别与椭圆方程联立,求出
方程,分别与椭圆方程联立,求出![]() 两点坐标,代入斜率公式,求出直线
两点坐标,代入斜率公式,求出直线![]() 的斜率,然后再判断与直线
的斜率,然后再判断与直线![]() 是否平行.
是否平行.
(1)∵椭圆过点D(![]() ,
,![]() ),且离心率为
),且离心率为![]()
![]()
∴![]() ,
,
∴椭圆的方程为![]() 1.
1.
(2)①由(1)知A(﹣2,0),B(0,1),
直线OD方程为y![]() ,
,
点P在直线OD上,设P(﹣2y0,y0),
kPAkPB![]() .
.
②设E(x1,y1),Q(x2,y2),
联立直线AP:y![]() 与椭圆的方程得,
与椭圆的方程得,
(2y02﹣2y0+1)x2+4y02x+8y0﹣4=0,
∴﹣2+x1![]() ,
,
∴x1![]() ,y1
,y1![]() ,
,
联立直线BP:y![]() 与椭圆的方程得,
与椭圆的方程得,
![]() ,
,
∴x2![]() ,y2
,y2![]() ,
,
∴![]()
又因为kAB![]() ,∴kAB=kEQ,
,∴kAB=kEQ,
∴直线AB与EQ是平行.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目