��Ŀ����
����Ŀ��ijУΪ���������ѡ�ε�ѡ���������Ա��ϵ�������ȡ50��ѧ�����õ���������ݱ���
����ƽ�漸��ѡ���� | ��������ϵ��������̡� | ������ʽѡ���� | �ϼ� | |
���� | 16 | 4 | 6 | 26 |
�� | 4 | 8 | 12 | 24 |
�ϼ� | 20 | 12 | 18 | 50 |
��1�����ݱ����ṩ�����ݣ�ѡ���ֱ���жϡ�ѡ���������Ա��й�ϵ�������֣���Ϊѡ������ı�����ȡֵ��������������ѡ���������Ա��й�ϵ�İ��մ�
����K2= ![]() ��
��
P��k2��k0�� | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
��2���ڳ�ȡ��50��ѧ���У����շֲ�����ķ�����������ƽ�漸��ѡ��������������ϵ��������̡���ѧ���г�ȡ8�˽����ʾ���������8������ѡ3�ˣ�������ƽ�漸��ѡ������������ȥ����������ϵ��������̡��������IJ�Ϊ�Σ���εķֲ��м���ѧ������
���𰸡�
��1���⣺ѡ��������ϵ��������̡���������ʽѡ������k=0������������ѡ�����Ա��أ�
ѡ��������ϵ��������̡�������ƽ�漸��ѡ������K2= ![]() ��6.969��6.635��
��6.969��6.635��
����99%�İ�����Ϊѡ��������ϵ��������̡�������ƽ�漸��ѡ�������Ա��йأ�
ѡ����ƽ�漸��ѡ������������ʽѡ������K2= ![]() ��8.464��7.879��
��8.464��7.879��
����99.5%�İ�����Ϊѡ����ƽ�漸��ѡ������������ʽѡ�������Ա��йأ�
����������ѡ����ƽ�漸��ѡ������������ʽѡ�������Ա��йصİ������
��2���⣺����ƽ�漸��ѡ��������������ϵ��������̡���ѧ�������ı���Ϊ20��12=5��3�����г�ȡ8�˽����ʾ��������ֱ�Ϊ5��3��
�����⣬��=��3����1��1��3����
P����=��3��= ![]() =
= ![]() ��P����=��1��=
��P����=��1��= ![]() =
= ![]() ��P����=1��=
��P����=1��= ![]() =
= ![]() ��P����=1��=
��P����=1��= ![]() =
= ![]() ��
��
�εķֲ���
�� | ��3 | ��1 | 1 | 3 |
P |
|
|
|
|
��ѧ����E��=����3���� ![]() +����1����
+����1���� ![]() +1��
+1�� ![]() +3��
+3�� ![]() =
= ![]()
����������1������K2= ![]() �����K2 �� ���ٽ�ֵ�Ƚϣ����ɵó����ۣ���2������ƽ�漸��ѡ��������������ϵ��������̡���ѧ�������ı���Ϊ20��12=5��3�����г�ȡ8�˽����ʾ��������ֱ�Ϊ5��3�������⣬��=��3����1��1��3�������Ӧ�ĸ��ʣ�������εķֲ��м���ѧ������
�����K2 �� ���ٽ�ֵ�Ƚϣ����ɵó����ۣ���2������ƽ�漸��ѡ��������������ϵ��������̡���ѧ�������ı���Ϊ20��12=5��3�����г�ȡ8�˽����ʾ��������ֱ�Ϊ5��3�������⣬��=��3����1��1��3�������Ӧ�ĸ��ʣ�������εķֲ��м���ѧ������

����Ŀ������Դ�����Ĵ������ˣ�2018��3��5�����磬���ǿ������������������ʱ��ʾ��������Դ������������˰�Ż��������ӳ����꣬��2018��1��1����2020��12��31�գ��Թ��õ�����Դ����������������˰.ij�˼ƻ���2018��5�¹���һ��ijƷ������Դ���������ӵ��ظ�Ʒ��������վ�˽�������ʵ���������±���
�·� | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
�·ݱ��t | 1 | 2 | 3 | 4 | 5 |
������������ | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
��1�����������������Իع�ģ����ϵ��ظ�Ʒ������Դ����ʵ������![]() �����������·ݱ��
�����������·ݱ��![]() ֮�����ع�ϵ.������С���˷���
֮�����ع�ϵ.������С���˷���![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ����Ԥ��2018��5�·ݵ��ظ�Ʒ������Դ������������
����Ԥ��2018��5�·ݵ��ظ�Ʒ������Դ������������
��2��2018��6��12�գ���������͵ط���������������Դ���������������̣�����Դ������������������ָ����������Դ������װ��ȼ�ϻ������ܹ��ṩ�����ܵ���Զ��̣��Թ�������������һ�ֵ���.��֪ij���������Դ����������Ⱥ��ʮ���Ӵ�ij���л��������е�200�������ߵĹ���������������Ԥ��ֵ������һ���������飬�õ�����һ��Ƶ������
�������Ԥ��ֵ���䣨��Ԫ�� |
|
|
|
|
|
|
20 | 60 | 60 | 30 | 20 | 10 |
��Ƶ����Ϊ���ʣ�����������������Ӹõ����������Դ�����������������������ȡ3�ˣ��DZ���ȡ3���жԲ�����������Ԥ��ֵ������3��Ԫ������Ϊ![]() ����
����![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() .
.
�ο���ʽ�����ݣ��ٻع鷽��![]() ������
������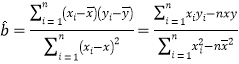 ��
��![]() ����
����![]() ��.
��.
����Ŀ�����Ӵ�ý��˾Ϊ�˽����籭�ڼ�ij�������ӹ��ڶԡ�ս��������Ŀ����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ��ý�Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ��

(ע��Ƶ�ʷֲ�ֱ��ͼ������![]() ��ʾ
��ʾ![]() �����磬�տ�ʱ����
�����磬�տ�ʱ����![]() ���ӵ�Ƶ����
���ӵ�Ƶ����![]() )
)
���վ��տ��������Ŀʱ�䲻����40���ӵĹ��ڳ�Ϊ�������ԡ���
��1��������֪������������![]() �����������ݴ������ж��Ƿ������Ϊ�������ԡ����Ա��йأ�����йأ��ж����գ�
�����������ݴ������ж��Ƿ������Ϊ�������ԡ����Ա��йأ�����йأ��ж����գ�
�������� | ������ | �ϼ� | |
�� | |||
Ů | 10 | 55 | |
�ϼ� |
��2���������������õ���Ƶ����Ϊ���ʣ����ڴӸõ����������ӹ����У����������������ÿ�γ�ȡ1�����ڣ���ȡ3�Σ��DZ���ȡ��3�������еġ������ԡ�����Ϊ![]() ����ÿ�γ�ȡ�Ľ����������ģ���
����ÿ�γ�ȡ�Ľ����������ģ���![]() �ķֲ��С���ֵ
�ķֲ��С���ֵ![]() �ͷ���
�ͷ���![]() ��
��
����![]() ��
��
|
|
|
|
|
|
|
|
|
|

