题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若对任意![]() ,函数
,函数![]() 的图像不在
的图像不在![]() 轴上方,求
轴上方,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)对函数求导,分当![]() 时和当
时和当![]() 时,讨论导函数的正负,进而得到单调区间;(2)原式子等价于对任意
时,讨论导函数的正负,进而得到单调区间;(2)原式子等价于对任意![]() ,都有
,都有![]() 恒成立,即在
恒成立,即在![]() 上
上![]() ,按照第一问分的情况,继续讨论导函数的正负得到原函数的单调性,进而得到函数的最值,得到结果.
,按照第一问分的情况,继续讨论导函数的正负得到原函数的单调性,进而得到函数的最值,得到结果.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]()
![]()
![]() .
.
当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() (舍去),
(舍去),
则由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)对任意![]() ,函数
,函数![]() 的图像不在
的图像不在![]() 轴上方,等价于对任意
轴上方,等价于对任意![]() ,都有
,都有![]() 恒成立,即在
恒成立,即在![]() 上
上![]() .
.
由(1)知,当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
又![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() 在
在![]() 处取得极大值也是最大值,
处取得极大值也是最大值,
所以![]() .
.
令![]() ,所以
,所以![]() .
.
在![]() 上,
上,![]() ,
,![]() 是减函数.
是减函数.
又![]() ,所以要使得
,所以要使得![]() ,须
,须![]() ,即
,即![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.

【题目】未了解人们对“延迟退休年龄政策”的态度,某部门从年龄在15岁到65岁的人群中随机调查了100人,将这100人的年龄数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,整理得到如图所示的频率分布直方图.
,整理得到如图所示的频率分布直方图.
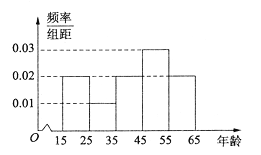
在这100人中不支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
不支持“延迟退休”的人数 | 15 | 5 | 15 | 23 | 17 |
(1)由频率分布直方图,估计这100人年龄的平均数;
(2)由频率分布直方图,若在年龄![]() ,
,![]() ,
,![]() 的三组内用分层抽样的方法抽取12人做问卷调查,求年龄在
的三组内用分层抽样的方法抽取12人做问卷调查,求年龄在![]() 组内抽取的人数;
组内抽取的人数;
(3)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异?
列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异?
\ | 45岁以下 | 45岁以上 | 总计 |
不支持 | |||
支持 | |||
总计 |
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
第一种生产方式 | 第二种生产方式 | |||||||||||||||||||
8 | 6 | 5 | 5 | 6 | 8 | 9 | ||||||||||||||
9 | 7 | 6 | 2 | 7 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 6 | 8 | ||||||
9 | 8 | 7 | 7 | 6 | 5 | 4 | 3 | 3 | 2 | 8 | 1 | 4 | 4 | 5 | ||||||
2 | 1 | 1 | 0 | 0 | 9 | 0 | ||||||||||||||
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
超过m | 不超过m | 总计 | |
第一种生产方式 | |||
第二种生产方式 | |||
总计 |
(3)根据(2)中的列表,能否有99%的把握认为两种生产方式的效率有差异?
附: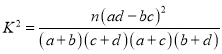 ,
,![]() .
.
【题目】某班随机抽查了![]() 名学生的数学成绩,分数制成如图的茎叶图,其中
名学生的数学成绩,分数制成如图的茎叶图,其中![]() 组学生每天学习数学时间不足
组学生每天学习数学时间不足![]() 个小时,
个小时,![]() 组学生每天学习数学时间达到一个小时,学校规定
组学生每天学习数学时间达到一个小时,学校规定![]() 分及
分及![]() 分以上记为优秀,
分以上记为优秀,![]() 分及
分及![]() 分以上记为达标,
分以上记为达标,![]() 分以下记为未达标.
分以下记为未达标.

(1)根据茎叶图完成下面的列联表:
达标 | 未达标 | 总计 | |
| |||
| |||
总计 |
(2)判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】新冠状病毒严重威胁着人们的身体健康,我国某医疗机构为了调查新冠状病毒对我国公民的感染程度,选了某小区的![]() 位居民调查结果统计如下:
位居民调查结果统计如下:
感染 | 不感染 | 合计 | |
年龄不大于 |
| ||
年龄大于 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为感染新冠状病与不同年龄有关?
的前提下认为感染新冠状病与不同年龄有关?
(3)已知在被调查的年龄大于![]() 岁的感染者中有
岁的感染者中有![]() 名女性,其中
名女性,其中![]() 位是女教师,现从这
位是女教师,现从这![]() 名女性中随机抽取
名女性中随机抽取![]() 人,求至多有
人,求至多有![]() 位教师的概率.
位教师的概率.
附: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如图的列联表:
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量![]() ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式![]()
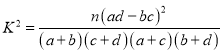 ,其中
,其中![]() )
)