Question

【题目】已知曲线的极坐标方程为，以极点为平面直角坐标系的原点，极轴为轴的正半轴，建立平面直角坐标系.

（1）若曲线：（t为参数）与曲线相交于两点，，求；

（2）若是曲线上的动点，且点的直角坐标为，求的最大值.

Answer 1

【答案】（1）（2）

【解析】

（1）曲线的极坐标方程为，化为，结合极坐标与直角坐标的互化公式可得曲线的直角坐标方程；由曲线：（为参数），消去参数，可得曲线的普通方程.求出圆心到直线的距离，再由垂径定理求解弦长；

（2）在曲线上，设（为参数），利用三角函数求的最大值.

（1）曲线的极坐标方程为，化为，

极坐标与直角坐标的互化公式：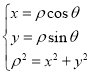

可得直角坐标方程为，

由曲线：（为参数），消去参数，

可得曲线的普通方程为，

圆的圆心坐标为，到直线的距离.

根据几何关系可得：弦长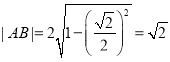

（2）在曲线上，

由（1）可得：

设（为参数），

则，其中，

的最大值为.