题目内容
(本小题满分12分)
如图,三棱锥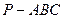 中,
中, 底面
底面 于
于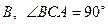 ,
,
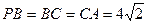 ,点
,点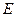 ,点
,点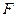 分别是
分别是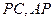 的中点.
的中点.

(1) 求证:侧面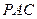 ⊥侧面
⊥侧面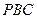 ;
;
(2) 求点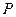 到平面
到平面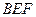 的距离;
的距离;
(3) 求异面直线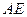 与
与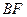 所成的角的余弦.
所成的角的余弦.
如图,三棱锥
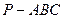 中,
中, 底面
底面 于
于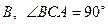 ,
,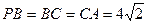 ,点
,点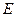 ,点
,点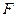 分别是
分别是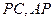 的中点.
的中点.
(1) 求证:侧面
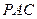 ⊥侧面
⊥侧面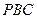 ;
;(2) 求点
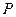 到平面
到平面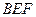 的距离;
的距离;(3) 求异面直线
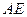 与
与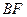 所成的角的余弦.
所成的角的余弦.(1)证明略
(2)4
(3)
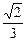
(1)以
 所在直线为
所在直线为 轴,
轴,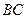 所在直线
所在直线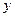 轴,建立空间直角坐标系,由条件可设
轴,建立空间直角坐标系,由条件可设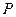 (0,0,4
(0,0,4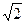 ),
), 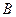 (0,0,0),
(0,0,0), 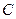 (0,–4
(0,–4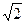 ,0),
,0), (4
(4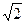 ,–4
,–4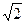 ,0);
,0);则
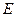 (0,–2
(0,–2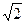 ,2
,2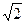 ),
),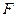 (2
(2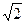 ,–2
,–2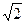 ,2
,2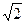 ), --- 2分
), --- 2分平面
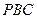 的法向量
的法向量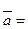 (1,0,0 ), 而
(1,0,0 ), 而 ,
,因为
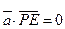 , 所以侧面
, 所以侧面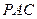 ⊥侧面
⊥侧面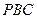 ; --- 2分
; --- 2分(或 ∵
 底面
底面 , ∴ 平面
, ∴ 平面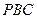 ⊥平面
⊥平面 , --- 2分
, --- 2分又∵
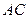 ⊥
⊥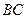 ,∴
,∴ 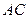 ⊥平面
⊥平面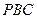 , ∴ 侧面
, ∴ 侧面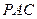 ⊥侧面
⊥侧面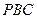 ;) . --- 2分
;) . --- 2分(2) 在等腰直角三角形
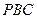 中,
中, 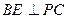 , 又中位线
, 又中位线 , 而由(1)
, 而由(1)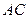 ⊥平面
⊥平面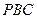 , 则
, 则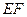 ⊥平面
⊥平面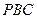 , ∴
, ∴  , --- 2分
, --- 2分所以
 平面
平面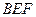 , 那么线段
, 那么线段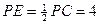 即为点
即为点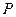 到平面
到平面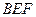 的距离. --- 2分
的距离. --- 2分(3)由(1)所建坐标系, 得
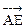 =(–4
=(–4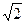 ,2
,2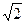 ,2
,2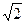 ),
), 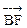 =(2
=(2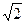 ,–2
,–2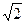 ,2
,2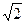 ),
),∴
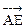 ·
·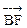 ="–16," 又|
="–16," 又|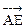 |·|
|·|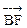 |=24
|=24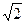 , --- 2分
, --- 2分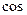 <
<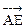 ,
,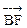 >=–
>=–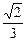 ,
, ∴
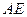 与
与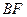 所成的角的余弦值是
所成的角的余弦值是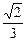 . --- 2分
. --- 2分
练习册系列答案
相关题目
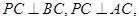 点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。
点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。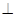 平面ABC
平面ABC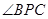 是直线EF与直线PC所成的角
是直线EF与直线PC所成的角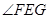 是平面PAB与平面ABC所成二面角的平面角
是平面PAB与平面ABC所成二面角的平面角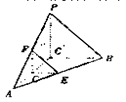
 中,底面
中,底面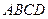 是
是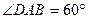 的菱形,
的菱形,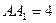 ,
,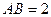 ,点
,点 在棱
在棱 上,点
上,点 是棱
是棱 的中点.
的中点.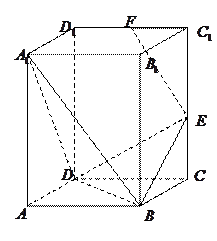
 ;
; 的长度,使得
的长度,使得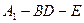 为直二面角.
为直二面角. 中,棱长为
中,棱长为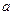
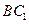 与
与 所成的角;
所成的角;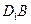 与平面
与平面 所成角的正切值;
所成角的正切值;
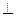 平面
平面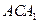 .
.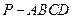 的底面为直角梯形,
的底面为直角梯形,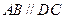 ,
,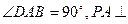 底面
底面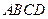 ,且
,且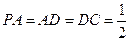 ,
,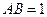 ,
,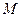 是
是 的中点。
的中点。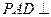 面
面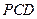 ;
; 与
与 与面
与面 所成二面角的余弦值.
所成二面角的余弦值.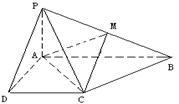
 中,
中, 底面
底面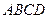 ,
,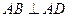 ,
,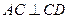 ,
,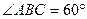 ,
,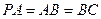 ,
,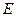 是
是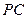 的中点.
的中点.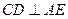 ;
;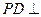 面
面 ;
;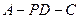 的平面角的正弦值.
的平面角的正弦值.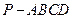 中,底面
中,底面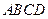 是矩形,
是矩形,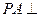 平面
平面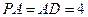 ,
,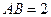 . 以
. 以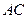 的中点
的中点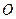 为球心、
为球心、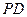 于点
于点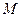 ,交
,交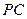 于点
于点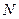 .
.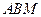 ⊥平面
⊥平面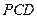 ;
;
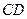 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.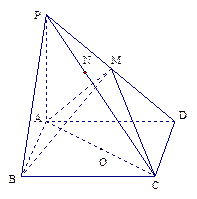
 AB-C2为60o,
AB-C2为60o, 则点C
则点C 1与C2之间的距离可能是___________.(写出二个可能值即可)
1与C2之间的距离可能是___________.(写出二个可能值即可) 的等边三角形,另外两个面是等腰直角三角形,则这个三棱锥的体积为
的等边三角形,另外两个面是等腰直角三角形,则这个三棱锥的体积为