题目内容
【题目】已知函数f（x）=|x2﹣2ax+b|（x∈R），给出下列命题：
①a∈R，使f（x）为偶函数；
②若f（0）=f（2），则f（x）的图象关于x=1对称；
③若a2﹣b≤0，则f（x）在区间[a，+∞）上是增函数；
④若a2﹣b﹣2＞0，则函数h（x）=f（x）﹣2有2个零点．
其中正确命题的序号为 ．
【答案】①③
【解析】解：①当a=0时，f（x）=|x2+b|显然是偶函数，故①正确；
②取a=0，b=﹣2，函数f（x）=|x2﹣2ax+b|化为f（x）=|x2﹣2|，满足f（0）=f（2），
但f（x）的图象不关于x=1对称，故②错误；
③若a2﹣b≤0，则f（x）=|（x﹣a）2+b﹣a2|=（x﹣a）2+b﹣a2在区间[a，+∞）上是增函数，故③正确；
④h（x）=|（x﹣a）2+b﹣a2|﹣2有4个零点，故④错误．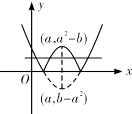
∴正确命题为①③．
所以答案是：①③．
【考点精析】根据题目的已知条件，利用命题的真假判断与应用的相关知识可以得到问题的答案，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．
练习册系列答案
相关题目
【题目】假设关于某设备的使用年限
（年）和所支出的维修费用
（万元）有如下统计资料：
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知， 
对
呈线性相关关系，试求：
（1）回归直线方程；
（2）估计使用年限为10年时，维修费用约是多少？
参考公式：回归直线方程： 
.其中
（注： 
)
