题目内容
9．已知点P为椭圆x2+2y2=98上一个动点，A（0，5），求|PA|的最值．分析 可设P（7$\sqrt{2}$cosα，7sinα），0≤α＜2π，A（0，5），即有|PA|=$\sqrt{（7\sqrt{2}cosα）^{2}+（7sinα-5）^{2}}$，再由同角的平方关系和正弦函数的值域，配方即可得到所求最值．
解答 解：点P为椭圆x2+2y2=98上一个动点，
可设P（7$\sqrt{2}$cosα，7sinα），0≤α＜2π，
A（0，5），即有|PA|=$\sqrt{（7\sqrt{2}cosα）^{2}+（7sinα-5）^{2}}$
=$\sqrt{-49si{n}^{2}α-70sinα+123}$
=$\sqrt{-49（sinα+\frac{5}{7}）^{2}+148}$，
由-1≤sinα≤1，可得sinα=-$\frac{5}{7}$时，|PA|取得最大值2$\sqrt{37}$；
当sinα=1，即α=$\frac{π}{2}$时，|PA|取得最小值2．
点评 本题考查椭圆的参数方程的运用，考查三角函数的化简和求值，注意运用同角的平方关系和正弦函数的值域，属于中档题．
练习册系列答案
相关题目
1．
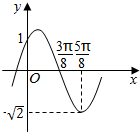函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ≤$\frac{π}{2}$）的图象如图所示，将f（x）的图象向左平移$\frac{π}{8}$个单位后得到函数g（x）的图象，则（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ≤$\frac{π}{2}$）的图象如图所示，将f（x）的图象向左平移$\frac{π}{8}$个单位后得到函数g（x）的图象，则（ ）| A． | g（x）=$\sqrt{2}$sin（2x+$\frac{3π}{8}$） | B． | g（x）=$\sqrt{2}$cos2x | C． | g（x）=$\sqrt{2}$cos（2x+$\frac{3π}{8}$） | D． | g（x）=$\sqrt{2}$sin2x |