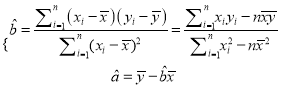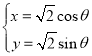题目内容
【题目】选修4—4：坐标系与参数方程.
已知曲线
的参数方程为
（
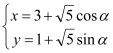为参数），以直角坐标系原点为极点，
轴正半轴为极轴建立极坐标系.
（1）求曲线的极坐标方程；
（2）若直线的极坐标方程为
，求直线被曲线截得的弦长.
【答案】（1） 
（2）
【解析】
试题分析：（1） 利用
，即可把参数方程转化为平面直角坐标系方程，然后在利用
就可以把方程化成极坐标方程；
（2）由（1）知曲线
的平面直角坐标系方程为圆的方程，直线的极坐标方程为
为直线
，然后利用弦长公式就可求解.
试题解析：
∵曲线
的参数方程为
（
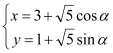为参数）
∴曲线的普通方程为
曲线
表示以
为圆心，
为半径的圆。
将
代入并化简：
即曲线
的极坐标方程为 .
∵的直角坐标方程为
∴圆心到直线的距离为
∴弦长为 .
练习册系列答案
相关题目
【题目】葫芦岛市某高中进行一项调查：2012年至2016年本校学生人均年求学花销
（单位：万元）的数据如下表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
（1）求
关于
的线性回归方程；
（2）利用（1）中的回归方程，分析2012年至2016年本校学生人均年求学花销的变化情况，并预测该地区2017年本校学生人均年求学花销情况．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
