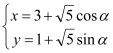题目内容
【题目】已知函数![]() ,
, ![]() ,
, ![]() 的解集为
的解集为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)m=3;(2)t≤1或t≥![]()
【解析】【试题分析】(1)依据题设条件运用绝对值的定义进行化简求解;(2)借助(1)的结论,先将问题等价转化,再建立不等式进行求解:
解:(I)∵函数f(x)=|x+3|﹣m+1,m>0, f(x﹣3)≥0的解集为(﹣∞,﹣2]∪[2,+∞).
所以f(x﹣3)=|x|﹣m+1≥0,
所以|x|≥m﹣1的解集为为(﹣∞,﹣2]∪[2,+∞).所以m﹣1=2,所以m=3;
(II)由(I)得f(x)=|x+3|﹣2
∵x∈R,f(x)≥|2x﹣1|﹣t2+![]() t 成立
t 成立
即x∈R,|x+3|﹣|2x﹣1|≥﹣t2+![]() t+2成立
t+2成立
令g(x)=|x+3|=|2x﹣1|=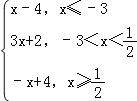
故g(x)max=g(![]() )=
)=![]()
则有![]() |≥﹣t2+
|≥﹣t2+![]() t+2,即|2t2﹣5t+3≥0.
t+2,即|2t2﹣5t+3≥0.
解得t≤1或t≥![]() ,∴实数t的取值范围是t≤1或t≥
,∴实数t的取值范围是t≤1或t≥![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目