题目内容
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点至少有一个在原点右侧.
轴的交点至少有一个在原点右侧.
(1)求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,求
,求![]() 的值(其中
的值(其中![]() 表示不超过
表示不超过![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() );
);
(3)对(2)中的![]() 求函数
求函数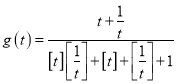 的值域.
的值域.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)分![]() 和
和![]() 两种情况讨论,在
两种情况讨论,在![]() 时进行验证即可,在
时进行验证即可,在![]() 时,由
时,由![]() 可分二次函数
可分二次函数![]() 有且只有一个零点且为正零点、一个正零点和一个负零点、两个正零点三种情况进行分类讨论,由此可得出实数
有且只有一个零点且为正零点、一个正零点和一个负零点、两个正零点三种情况进行分类讨论,由此可得出实数![]() 的取值范围;
的取值范围;
(2)求出![]() ,可得出
,可得出![]() ,然后分
,然后分![]() 和
和![]() 两种情况讨论,根据定义得出
两种情况讨论,根据定义得出![]() 的值;
的值;
(3)分![]() 、
、![]() 、
、![]() 三种情况讨论,在
三种情况讨论,在![]() 时代入函数
时代入函数![]() 的解析式计算即可,在
的解析式计算即可,在![]() 时,利用函数
时,利用函数![]() 的单调性得出该函数的值域,在
的单调性得出该函数的值域,在![]() 时,考查
时,考查![]() ,结合函数的单调性来得出值域,由此可得出函数
,结合函数的单调性来得出值域,由此可得出函数![]() 的值域.
的值域.
(1)①若![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,此时,函数
,此时,函数![]() 只有一个正零点,合乎题意;
只有一个正零点,合乎题意;
②若![]() ,由于
,由于![]() .
.
(i)若函数![]() 有且只有一个零点且为正数,则
有且只有一个零点且为正数,则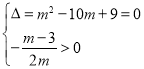 ,解得
,解得![]() ;
;
(ii)若函数![]() 有一个正零点和一个负零点,则
有一个正零点和一个负零点,则![]() ,解得
,解得![]() ;
;
(iii)若函数![]() 有两个正零点时,则
有两个正零点时,则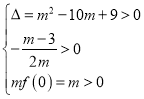 ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)![]() ,
,![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() ;当
;当![]() 时,
时,![]() ,此时
,此时![]() .
.
因此,![]() ;
;
(3)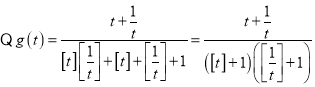 .
.
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,
,![]() ,则
,则![]() 单调递增,此时
单调递增,此时![]() ;
;
③当![]() 时,设
时,设![]() ,则
,则![]() ,
,![]() ,
,
此时,![]() 在
在![]() 上单调递增,则
上单调递增,则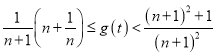 .
.
设![]() ,
,
则![]()
![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 且
且![]() 时,
时,![]() ,数列
,数列![]() 单调递增,
单调递增,![]() ;
;
设![]() ,当
,当![]() 且
且![]() ,数列
,数列![]() 单调递增,
单调递增,
当![]() 时,
时,![]() .
.
所以,当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() .
.
综上所述,函数![]() 的值域为
的值域为![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目