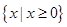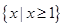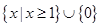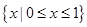题目内容
如图,两个工厂A、B相距2km,点O为AB的中点,要在以O为圆心,2km为半径的圆弧MN上的某一点P处建一幢办公楼,其中MA⊥AB,NB⊥AB.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比,比例系数为1;办公楼受工厂B的“噪音影响度”与距离BP的平方也成反比,比例系数为4,办公楼与A、B两厂的“总噪音影响度”y是A、B两厂“噪音影响度”的和,设AP为xkm.
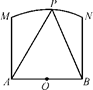
(1)求“总噪音影响度”y关于x的函数关系式,并求出该函数的定义域;
(2)当AP为多少时,“总噪音影响度”最小?

(1)求“总噪音影响度”y关于x的函数关系式,并求出该函数的定义域;
(2)当AP为多少时,“总噪音影响度”最小?
(1)y= (
( ≤x≤
≤x≤ )(2)AP=
)(2)AP= km
km
 (
( ≤x≤
≤x≤ )(2)AP=
)(2)AP= km
km(1)(解法1)如图,连结OP,

设∠AOP=α,则 ≤α≤
≤α≤ .
.
在△AOP中,由余弦定理得x2=12+22-2×1×2cosα=5-4cosα,
在△BOP中,由余弦定理得BP2=12+22-2×1×2cos(π-α)=5+4cosα,
∴BP2=10-x2,∴y= .
.
∵ ≤α≤
≤α≤ ,∴
,∴ ≤x≤
≤x≤ ,∴y=
,∴y= (
( ≤x≤
≤x≤ ).
).

(解法2)建立如图所示的直角坐标系,则A(-1,0),B(1,0),设P(m,n),则PA2=(m+1)2+n2,PB2=(m-1)2+n2.
∵m2+n2=4,PA=x,
∴PB2=10-x2(后面解法过程同解法1).
(2)(解法1)y= =
=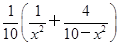 [x2+(10-x2)]
[x2+(10-x2)]
= (5+
(5+ )≥
)≥ (5+2
(5+2 )=
)=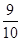 ,
,
当且仅当 ,即x=
,即x= ∈[
∈[ ,
, ]时取等号.
]时取等号.
故当AP= km时,“总噪音影响度”最小.
km时,“总噪音影响度”最小.
(解法2)由y= ,得
,得
y′=- .
.
∵ ≤x≤
≤x≤ ,∴令y′=0,得x=
,∴令y′=0,得x= ,且当x∈
,且当x∈ 时,y′<0;当x∈(
时,y′<0;当x∈( ,
, ]时,y′>0.∴x=
]时,y′>0.∴x= 时,y=
时,y= 取极小值,也即最小值.故当AP=
取极小值,也即最小值.故当AP= km时,“总噪音影响度”最小
km时,“总噪音影响度”最小

设∠AOP=α,则
 ≤α≤
≤α≤ .
.在△AOP中,由余弦定理得x2=12+22-2×1×2cosα=5-4cosα,
在△BOP中,由余弦定理得BP2=12+22-2×1×2cos(π-α)=5+4cosα,
∴BP2=10-x2,∴y=
 .
.∵
 ≤α≤
≤α≤ ,∴
,∴ ≤x≤
≤x≤ ,∴y=
,∴y= (
( ≤x≤
≤x≤ ).
).
(解法2)建立如图所示的直角坐标系,则A(-1,0),B(1,0),设P(m,n),则PA2=(m+1)2+n2,PB2=(m-1)2+n2.
∵m2+n2=4,PA=x,
∴PB2=10-x2(后面解法过程同解法1).
(2)(解法1)y=
 =
=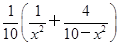 [x2+(10-x2)]
[x2+(10-x2)]=
 (5+
(5+ )≥
)≥ (5+2
(5+2 )=
)=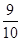 ,
,当且仅当
 ,即x=
,即x= ∈[
∈[ ,
, ]时取等号.
]时取等号.故当AP=
 km时,“总噪音影响度”最小.
km时,“总噪音影响度”最小.(解法2)由y=
 ,得
,得y′=-
 .
.∵
 ≤x≤
≤x≤ ,∴令y′=0,得x=
,∴令y′=0,得x= ,且当x∈
,且当x∈ 时,y′<0;当x∈(
时,y′<0;当x∈( ,
, ]时,y′>0.∴x=
]时,y′>0.∴x= 时,y=
时,y= 取极小值,也即最小值.故当AP=
取极小值,也即最小值.故当AP= km时,“总噪音影响度”最小
km时,“总噪音影响度”最小
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
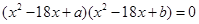 的4个实数根构成以d为公差的等差数列,若
的4个实数根构成以d为公差的等差数列,若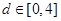 ,则
,则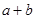 的取值范围是 .
的取值范围是 .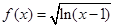 的定义域是( )
的定义域是( )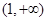
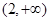
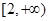
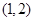
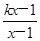 (k∈R,且k>0).
(k∈R,且k>0).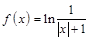 的值域是__________.
的值域是__________.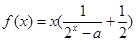 定义域为
定义域为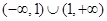 ,则满足不等式
,则满足不等式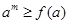 的实数m的集合____________
的实数m的集合____________ 的值域是____________.
的值域是____________.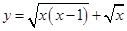 的定义域为( )
的定义域为( )